题目内容
7.设k为正整数,记k!=1×2×3×…×k,S=1!(12+1+1)+2!(22+2+1)+3!(32+3+1)+…+2014!(20142+2014+1),则$\frac{S+1}{2015!}$=2015.分析 根据题意化简得到n!(n2+n+1)=(n+1)•(n+1)!-n•n!,进而确定出S,代入原式计算即可得到结果.
解答 解:∵n!(n2+n+1)=n![(n+1)2-n]=(n+1)2n!-n•n!=(n+1)•(n+1)!-n•n!,
∴S=2•2!-1•1!+3•3!-2•2!+…+2015•2015!-2014•2014!=2015•2015!-1•1!,
则$\frac{S+1}{2015!}$=$\frac{2015•2015!}{2015!}$=2015.
故答案为:2015
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
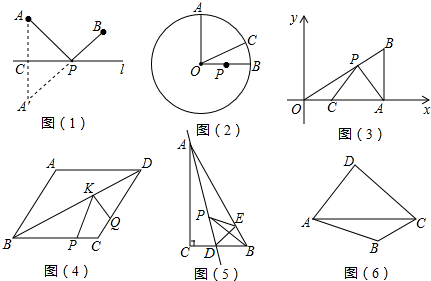
 图中有多少个三角形?
图中有多少个三角形?