题目内容
7.请画出函数y=-$\frac{1}{2}x$2+x+$\frac{5}{2}$的图象,并说明这个函数具有哪些性质?分析 可根据二次函数的解析式,列出函数经过的坐标,在直角坐标系中描出这些点,再用光滑的曲线顺次连接各点,即可画出函数的图象;可从函数的单调性以及最值方面来说明函数具有的性质.
解答 解:(1)列表:在x的取值范围内列出函数对应值表;
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -$\frac{3}{2}$ | 1 | 2$\frac{1}{2}$ | 3 | 2$\frac{1}{2}$ | 1 | -$\frac{3}{2}$ |
(3)连线:用光滑的曲线顺次连接各点,得到函数y=-$\frac{1}{2}x$2+x+$\frac{5}{2}$的图象.

则可得到这个函数的性质如下:
当x<1时,函数值y随x的增大而增大;当x>1时,函数值y随x的增大而减小;
当x=1时,函数取得最大值,最大值y=3.
点评 本题综合考查了二次函数的性质,同时应掌握由函数的几个关键点画函数图象.掌握正确的作图方法,画出抛物线的图象,得出有关性质.

练习册系列答案
相关题目
18.下列每组单项式中是同类项的是( )
| A. | a和0 | B. | 4x2和4x3 | C. | 5ab和-5bc | D. | -x2y3和5y3x2 |
15.学完了有理数这一章后,海州实验中学七年级的小聪同学用计算机设计了一个计算程序,如表.请问当输入数据是-9时,输出的结果是-$\frac{9}{82}$.
| 输入 | -1 | 2 | -3 | 4 | -5 | … |
| 输出 | -$\frac{1}{2}$ | $\frac{2}{5}$ | -$\frac{3}{10}$ | $\frac{4}{17}$ | -$\frac{5}{26}$ | … |
12.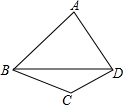 如图,四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=130°,则∠A的度数是( )
如图,四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=130°,则∠A的度数是( )
 如图,四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=130°,则∠A的度数是( )
如图,四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=130°,则∠A的度数是( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
 如图,A点坐标为(3,3),将△ABC先向下平移4个单位得△A1B1C1,再将△A1B1C1向左平移5个单位得△A2B2C2.
如图,A点坐标为(3,3),将△ABC先向下平移4个单位得△A1B1C1,再将△A1B1C1向左平移5个单位得△A2B2C2. 如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴的对称图形△A1B1C1,再画出△A1B1C1向右平移1个单位的△A2B2C2.
如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴的对称图形△A1B1C1,再画出△A1B1C1向右平移1个单位的△A2B2C2.