题目内容
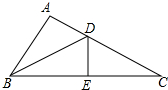 已知在△ABC中,∠A=90°,D,E分别是边BC,AC上的点,且DE⊥BC于D,△ADB≌△EDB≌EDC,则∠C的度数为多少?.DE与DC之间有怎样的数量关系?说明理由.
已知在△ABC中,∠A=90°,D,E分别是边BC,AC上的点,且DE⊥BC于D,△ADB≌△EDB≌EDC,则∠C的度数为多少?.DE与DC之间有怎样的数量关系?说明理由.考点:全等三角形的性质,含30度角的直角三角形
专题:
分析:根据全等三角形的象征得出∠A=∠DEB=∠DEC=90°,∠ABD=∠EBD=∠C,跟即三角形内角和定理求出∠C=30°,根据含30度角的就三角形性质得出即可.
解答:解:当∠C=30°时,△ADB≌△EDB≌EDC,DC=2ED,
理由是:∵△ADB≌△EDB≌△EDC,
∴∠A=∠DEB=∠DEC=90°,∠ABD=∠EBD=∠C,
∵∠A=90°,
∴∠C+∠ABC=90°,
∴3∠C=90°,
∴∠C=30°,
∵∠DEC=90°,
∴DC=2DE.
理由是:∵△ADB≌△EDB≌△EDC,
∴∠A=∠DEB=∠DEC=90°,∠ABD=∠EBD=∠C,
∵∠A=90°,
∴∠C+∠ABC=90°,
∴3∠C=90°,
∴∠C=30°,
∵∠DEC=90°,
∴DC=2DE.
点评:本题考查了全等三角形的性质,含30度角的直角三角形性质的应用,注意:全等三角形的对应边相等,题目比较好,难度适中.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
下列事件中,属于必然事件的是( )
| A、明天会下雨 |
| B、三角形两边之和大于第三边 |
| C、两个数的和大于每一个加数 |
| D、在一个没有红球的盒子里,摸到红球 |
一个数的平方是25,则这个数是( )
| A、5 | ||||
| B、-5 | ||||
| C、5或-5 | ||||
D、
|
下列变形中正确的是( )
| A、x2-(-x+y)=x2+x-y |
| B、3a-(b+c-d)=3a-b+c-d |
| C、4+2(a-b)=4+2a-b |
| D、a+(b-c)=ab-c |
下列各式中,去括号正确的是( )
| A、3-(a-b)=3-a+b |
| B、3-2(a-b)=3-2a+b |
| C、3+(a-b)=3+a+b |
| D、3-2(a-b)=3-2a-2b |
若|x+
|+(2y+1)2=0,则x2+y2的值是( )
| 1 |
| 2 |
| A、0 | ||
B、
| ||
C、
| ||
| D、1 |
下列各数中互为相反数的是( )
| A、-(+3)和+(-3) | ||
| B、-(-3)和-3 | ||
| C、(-2)3和-23 | ||
D、-3和
|
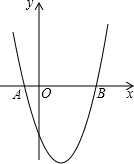 如图,抛物线y=x2-2x-3与x轴交于A、B两点,直线y=kx-1与抛物线交于P、Q两点,且y轴平分线段PQ,求k的值.
如图,抛物线y=x2-2x-3与x轴交于A、B两点,直线y=kx-1与抛物线交于P、Q两点,且y轴平分线段PQ,求k的值.