题目内容
11．计算：（$\frac{1}{a+1}-\frac{1}{1-a}$）$•\frac{a-1}{a}$．分析 先对括号内的式子进行通分，然后去括号，进行约分化简即可解得本题．
解答 解：（$\frac{1}{a+1}-\frac{1}{1-a}$）$•\frac{a-1}{a}$
=$\frac{（a-1）+（a+1）}{（a+1）（a-1）}•\frac{a-1}{a}$
=$\frac{a-1+a+1}{（a+1）（a-1）}•\frac{a-1}{a}$
=$\frac{2a}{（a+1）（a-1）}•\frac{a-1}{a}$
=$\frac{2}{a+1}$．
点评 本题考查分式的混合运算，解题的关键是明确分式通分、约分的方法．
练习册系列答案
相关题目
已知：如图，AB∥CD，点O是BC的中点，BE∥CF，BE、CF分别交AD于点E、F．
操作探究：
如图，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A．
16．
已知点P是边长为4的等边三角形边BC上一点，从点P向AB作垂线PQ，延长PQ与AC的延长线交于点R，设BP=x，$\frac{PQ+RQ}{PQ}=y$，则y关于x的大致图象是（ ）
已知点P是边长为4的等边三角形边BC上一点，从点P向AB作垂线PQ，延长PQ与AC的延长线交于点R，设BP=x，$\frac{PQ+RQ}{PQ}=y$，则y关于x的大致图象是（ ）| A． |  | B． |  | C． |  | D． |  |
3．
如图，在Rt△PQR中，∠PRQ=90°，RP=RQ，边RP在数轴上．点Q表示的数为1，点R表示的数为3，以Q为圆心，QP为半径画弧交数轴负半轴于点P1，则P1表示的是（ ）
如图，在Rt△PQR中，∠PRQ=90°，RP=RQ，边RP在数轴上．点Q表示的数为1，点R表示的数为3，以Q为圆心，QP为半径画弧交数轴负半轴于点P1，则P1表示的是（ ）| A． | -2 | B． | -2$\sqrt{2}$ | C． | 1-2$\sqrt{2}$ | D． | 2$\sqrt{2}$-1 |
20．⊙O的半径为2cm，若直线a上有一点到圆心的距离为2cm，则直线a和圆O的位置关系是（ ）
| A． | 相交 | B． | 相切 | C． | 相离 | D． | 相切或相交 |
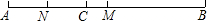（1）如图，线段AB=10cm，C是线段AB上的一点，AC=4cm，M是AB的中点，N是AC的中点，求线段MN的长；