题目内容
20．直线y=4x+1与抛物线y=x2+2x+k有唯一交点，则k=2．分析 直线y=4x+1与抛物线y=x2+2x+k有唯一交点，则把y=4x+1代入二次函数的解析式，得到的关于x的方程中，判别式△=0，据此即可求解．
解答 解：根据题意得：x2+2x+k=4x+1，
即x2-2x+（k-1）=0，
则△=4-4（k-1）=0，
解得：k=2．
故答案是：2．
点评 本题考查了二次函数与一次函数的交点个数的判断，把一次函数代入二次函数的解析式，得到的关于x的方程中，判别式△＞0则两个函数有两个交点，若△=0则只有一个交点，若△＜0则没有交点．
练习册系列答案
相关题目
11．四舍五入得到的近似数0.098，下列说法正确的是（ ）
| A． | 精确到万位 | B． | 精确到百分位 | C． | 精确到千分位 | D． | 精确到十分位 |
12．
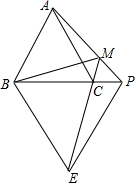如图，已知等边△ABC和等边△BPE，点P在BC的延长线上，EC的延长线交AP于M，连BM．若∠ABM=40°，则∠APB=（ ）
如图，已知等边△ABC和等边△BPE，点P在BC的延长线上，EC的延长线交AP于M，连BM．若∠ABM=40°，则∠APB=（ ）| A． | 40° | B． | 45° | C． | 50° | D． | 60° |
9．当n是正整数时，两个连续奇数的平方差（2n+1）2-（2n-1）2能被（ ）整除．
| A． | 6 | B． | 8 | C． | 12． | D． | 15 |
如图，已知∠AOB，求作射线OC，使OC平分∠AOB．