题目内容
10.解下列方程:|x+3|-|x-1|=x+1.分析 根据绝对值性质,去掉绝对值符号,题目应该分为三个取值范围进行讨论,分别为:x<-3,-3≤x≤1,x>1,去掉绝对值后,解三个一元一次方程.
解答 解:当x<-3时,
原方程得:-x-3+x-1=x+1,
解得:x=-5,满足x<-3,
∴x=-5.
当-3≤x≤1时,
原方程得:x+3+x-1=x+1,
解得:x=-1,满足-3≤x≤1,
∴x=-1.
当x>1时,
原方程得:x+3-x+1=x+1,
解得:x=3,满足x>1,
∴x=3.
∴方程的解为:x=-5、x=-1、x=3.
点评 题目考查了含有绝对值的一元次方程,解决此类问题的关键是去绝对值运算,因此涉及分类讨论问题.特别注意的是在每个讨论范围内,计算的方程的解要带回讨论区间验算,符合则保留,不符合要舍去.

练习册系列答案
相关题目
4.小敏到距家1500米的学校去上学,小敏出发10分钟后,小敏的爸爸立即去追小敏,且在距离学校60米的地方追上了她.已知爸爸比小敏的速度快100米/分,求小敏的速度.若设小敏的速度为x米/分,则根据题意所列方程正确的是( )
| A. | $\frac{1440}{x}=\frac{1440}{x+100}+10$ | B. | $\frac{1440}{x-100}-\frac{1440}{x}=10$ | ||
| C. | $\frac{1440}{x}=\frac{1440}{x-100}+10$ | D. | $\frac{1440}{x+100}-\frac{1440}{x}=10$ |
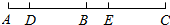 如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12.
如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12. 如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.
如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE. 如图,△DEF是由等腰△ABC经过平移得到的,其中AB=AC,且A与D、B与E、C与F分别是对应点,若∠B=50°,则∠D=80°.
如图,△DEF是由等腰△ABC经过平移得到的,其中AB=AC,且A与D、B与E、C与F分别是对应点,若∠B=50°,则∠D=80°.