题目内容
1.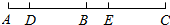 如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12.
如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12.(1)求线段AC的长;
(2)若M为AB的中点,N为BC的中点,求MN的长.
分析 (1)根据线段的和差,可得BD占AE的关系,根据解方程,可得AE的长,根据线段的和差,可得AB的长,根据线段中点的性质,可得答案;
(2)根据线段中点的性质,可得BM,BN的长,根据线段的和差,可得答案.
解答 解:(1)由线段的和差,得
BD=AE-AD-BE=AE-$\frac{1}{5}$AE-$\frac{1}{5}$AE=$\frac{3}{5}$AE.
又∵AE=12.
$\frac{3}{5}$AE=12.
解得AE=20,BE=$\frac{1}{5}$AE=4.
由线段的和差,得
AB=AE-BE=16.
由线段中点的性质,得
AC=2AB=32;
(2)由M为AB的中点,N为BC的中点,得
MB=$\frac{1}{2}$AB,NB=$\frac{1}{2}$BC.
由线段的和差,得
MN=$\frac{1}{2}$AB+$\frac{1}{2}$BC=$\frac{1}{2}$AB=$\frac{1}{2}$×32=16.
点评 本题考查了两点间的距离,利用线段的和差得出关于AE的方程是解题关键,又利用了线段的和差,线段中点的性质.

练习册系列答案
相关题目
11.小明近期几次数学测试成绩如下:第一次88分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分,那么小明第四次测验的成绩是( )
| A. | 93分 | B. | 78分 | C. | 94分 | D. | 84分 |

 苍溪嘉陵江三桥是连接苍溪老城与江南老区的一座下承式钢管混凝土柔性系杆拱桥,它的桥拱是抛物线形状,两桥墩的距离是240米,桥拱的拱高60米.
苍溪嘉陵江三桥是连接苍溪老城与江南老区的一座下承式钢管混凝土柔性系杆拱桥,它的桥拱是抛物线形状,两桥墩的距离是240米,桥拱的拱高60米.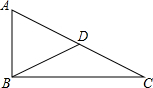 如图,Rt△ABC中∠ABC=90°,D为斜边AC的中点,AC=20cm,则BD=10cm.
如图,Rt△ABC中∠ABC=90°,D为斜边AC的中点,AC=20cm,则BD=10cm.