题目内容
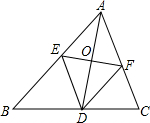 如图所示,△ABC中,D为BC上一个点,EF垂直平分AD交AB于E,交AC于F,若DE∥AC,判断四边形AEDF的形状并说明理由.
如图所示,△ABC中,D为BC上一个点,EF垂直平分AD交AB于E,交AC于F,若DE∥AC,判断四边形AEDF的形状并说明理由.考点:菱形的判定
专题:
分析:首先根据垂直平分线的性质可得AE=ED,AF=FD,AO=DO,证明△EDO≌△FAO可得AF=ED,进而得到AE=AF=ED=DF,再根据四边相等的四边形是菱形可得四边形AEDF是菱形.
解答:解:四边形AEDF是菱形,
理由:∵EF垂直平分AD交AB于E,
∴AE=ED,AF=FD,AO=DO,
∵DE∥AC,
∴∠FAD=∠EDA,
在△EDO和△FAO中
,
∴△EDO≌△FAO(ASA),
∴AF=ED,
∴AE=AF=ED=DF,
∴四边形AEDF是菱形.
理由:∵EF垂直平分AD交AB于E,
∴AE=ED,AF=FD,AO=DO,
∵DE∥AC,
∴∠FAD=∠EDA,
在△EDO和△FAO中
|
∴△EDO≌△FAO(ASA),
∴AF=ED,
∴AE=AF=ED=DF,
∴四边形AEDF是菱形.
点评:此题主要考查了菱形的判定,关键是掌握四边相等的四边形是菱形.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
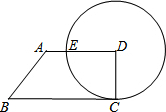 如图,已知四边形ABCD中,AD∥BC,∠C=90°,∠B=30°,以D为圆心,DC为半径的圆交AD于点E.若DC=4,BC=8+4
如图,已知四边形ABCD中,AD∥BC,∠C=90°,∠B=30°,以D为圆心,DC为半径的圆交AD于点E.若DC=4,BC=8+4 如图,长方形OABC的长OA为2,宽AB为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交负半轴于一点,则这个点表示的示数是
如图,长方形OABC的长OA为2,宽AB为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交负半轴于一点,则这个点表示的示数是