题目内容
15．
如图，已知AD⊥AB，AC⊥AE，AD=AB，∠C=∠E，DC交AB于点O，交BE于点P，AC交BE于点F．求证：DC⊥BE．
分析 根据全等三角形的判定证明即可．
解答 证明：∵AD⊥AB，AC⊥AE，
∴∠DAB=∠EAC，
∴∠DAB+∠BAC=∠EAC+∠BAC，
即∠DAC=∠EAB，
在△DAC与△EAB中，
$\left\{\begin{array}{l}{∠C=∠E}\\{AD=AC}\\{∠DAC=∠EAB}\end{array}\right.$，
∴△DAC≌△EAB（ASA），
∴∠D=∠B，
∵∠D+∠AOD=90°，∠AOD=∠BOP，
∴∠B+∠BOP=90°，
∴DC⊥BE．
点评 本题主要考查全等三角形的判定和性质，在判定三角形全等时，关键是选择恰当的判定条件．
练习册系列答案
相关题目
7．某厂接到加工720件衣服的订单，每天做48件正好按时完成，后因客户要求提前5天交货，设每天应多做x件，则x应满足的方程为（ ）
| A． | $\frac{720}{48}-\frac{720}{48+x}=5$ | B． | $\frac{720}{48}+5=\frac{720}{48+x}$ | C． | $\frac{720}{48}-\frac{720}{x}=5$ | D． | $\frac{720}{48+x}-\frac{720}{48}=5$ |
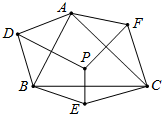如图，△ABC的内部有一点P，且点D、E、F是点P分别以AB、BC、AC所在直线为对称轴的对称点．若△ABC的内角∠BAC=70°，∠ABC=60°，∠ACB=50°，则∠ADB+∠BEC+∠CFA=360°．
在△ABC中，已知点D，E，F分别是BC、AD、CE的中点，且三角形ABC的面积等于4cm2，则三角形BEF的面积等于1cm2．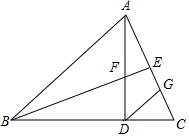
如图，在△ABC中，AB=BC，AD⊥BC于点D，点E为AC中点，连接BE交AD于点F，且BF=AC，过点D作DG∥AB，交AC于点G．