题目内容
18.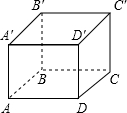 如图,长方体ABCD-A′B′C′D′中,AB=BB′=2,AD=3,一只蚂蚁从A点出发,沿长方体表面爬到C′点,求蚂蚁怎样走最短,最短路程是多少?
如图,长方体ABCD-A′B′C′D′中,AB=BB′=2,AD=3,一只蚂蚁从A点出发,沿长方体表面爬到C′点,求蚂蚁怎样走最短,最短路程是多少?
分析 做此题要把这个长方体中,蚂蚁所走的路线放到一个平面内,由于在平面内线段最短,根据勾股定理即可计算.
解答 解:如图1所示:
由题意得:AD=3,DC′=2+2=4,
在Rt△ADC′中,由勾股定理得AC′=$\sqrt{A{D}^{2}+DC{′}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
如图2所示: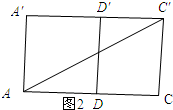
由题意得:AC=5,C′C=2,
在Rt△ACC′中,由勾股定理得;$AC′=\sqrt{A{C}^{2}+CC{′}^{2}}=\sqrt{{5}^{2}+{2}^{2}}$=$\sqrt{29}$,
∵$\sqrt{29}>5$.
∴第一种方法蚂蚁爬行的路线最短,最短路程是5.
点评 本题考查了平面展开-最短路径问题,此题的关键是明确线段最短这一知识点,然后把立体的长方体放到一个平面内,求出最短的路线.

练习册系列答案
相关题目
8.已知AB=A′B′,∠A=∠A′,∠B=∠B′,判断△ABC与△A′B′C′全等的根据是( )
| A. | SAS | B. | SSA | C. | ASA | D. | AAS |
10.下列命题中,是真命题的是( )
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 若a⊥b,b⊥c则a⊥c | |
| C. | 同旁内角相等,两直线平行 | |
| D. | 若a∥b,b∥c,则a∥c |
 如图,在△ABC中,点D在BC上,点E在AC上,AD交BE于F.已知EG∥AD交BC于G,EH⊥BE交BC于H,∠HEG=55°.
如图,在△ABC中,点D在BC上,点E在AC上,AD交BE于F.已知EG∥AD交BC于G,EH⊥BE交BC于H,∠HEG=55°. 如图所示,将长方形ABCD沿DE折叠,使点C恰好落在BA边上,得到点C′,若∠C′EB=40°,求∠EDC′的度数.
如图所示,将长方形ABCD沿DE折叠,使点C恰好落在BA边上,得到点C′,若∠C′EB=40°,求∠EDC′的度数.