题目内容
9. 如图,在△ABC中,点D在BC上,点E在AC上,AD交BE于F.已知EG∥AD交BC于G,EH⊥BE交BC于H,∠HEG=55°.
如图,在△ABC中,点D在BC上,点E在AC上,AD交BE于F.已知EG∥AD交BC于G,EH⊥BE交BC于H,∠HEG=55°.(1)求∠BFD的度数.
(2)若∠BAD=∠EBC,∠C=44°,求∠BAC的度数.
分析 (1)根据垂直的定义可得∠BEH=90°,然后求出∠BEG=35°,再根据两直线平行,同位角相等可得∠BFD=∠BEG;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BFD=∠EBC+∠ABE=∠ABC,然后根据三角形的内角和定理列式计算即可得解.
解答 解:(1)∵EH⊥BE,
∴∠BEH=90°,
∵∠HEG=55°,
∴∠BEG=35°,
又∵EG∥AD,
∴∠BFD=∠BEG=35°;
(2)∵∠BFD=∠BAD+∠ABE,∠BAD=∠EBC,
∴∠BFD=∠EBC+∠ABE=∠ABC=35°,
∵∠C=44°,
∴∠BAC=180°-∠ABC-∠C=180°-35°-44°=101°.
点评 本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,平行线的性质,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
19.下列方程中是一元二次方程的是( )
| A. | x2+2x=3 | B. | x2+y=0 | C. | (x2-2)2=9 | D. | x+$\frac{1}{x}$=3 |
 如图,已知△ACE≌△DBF,CE=BF,AE=DF,AD=8,BC=2,则AC=5.
如图,已知△ACE≌△DBF,CE=BF,AE=DF,AD=8,BC=2,则AC=5. △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示.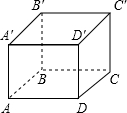 如图,长方体ABCD-A′B′C′D′中,AB=BB′=2,AD=3,一只蚂蚁从A点出发,沿长方体表面爬到C′点,求蚂蚁怎样走最短,最短路程是多少?
如图,长方体ABCD-A′B′C′D′中,AB=BB′=2,AD=3,一只蚂蚁从A点出发,沿长方体表面爬到C′点,求蚂蚁怎样走最短,最短路程是多少?