题目内容
16.计算(1)化简:$\frac{a+2b}{a+b}$÷$\frac{2{b}^{2}}{{a}^{2}-{b}^{2}}$
(2)解不等式组:$\left\{\begin{array}{l}{3(x+1)<5x}\\{\frac{1}{3}x-1≤7-\frac{5}{3}x}\end{array}\right.$.
分析 (1)原式利用除法法则变形,约分即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的方法部分即可.
解答 解:(1)原式=$\frac{a+2b}{a+b}$•$\frac{(a+b)(a-b)}{2{b}^{2}}$=$\frac{(a+2b)(a-b)}{2{b}^{2}}$;
(2)$\left\{\begin{array}{l}{3(x+1)<5x①}\\{\frac{1}{3}x-1≤7-\frac{5}{3}x②}\end{array}\right.$,
由①得:x>$\frac{3}{2}$,
由②得:x≤4,
则不等式组的解集为$\frac{3}{2}$<x≤4.
点评 此题考查了分式的乘除法,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
11.下列各图,是轴对称图形的有( )个.


| A. | 2 | B. | 3 | C. | 4 | D. | 4 |
 如图,在正方形ABCD中,对角线AC和BD相交于O,点E、F、G、H分别是OA、OB、OC、OD上,且AE=BF=CG=DH,求证:四边形EFGH是正方形.
如图,在正方形ABCD中,对角线AC和BD相交于O,点E、F、G、H分别是OA、OB、OC、OD上,且AE=BF=CG=DH,求证:四边形EFGH是正方形. 如图,D,E分别在等边三角形ABC中边CB和边BC的延长线上.
如图,D,E分别在等边三角形ABC中边CB和边BC的延长线上. 如图,将一枚硬币放到数轴上,把与数轴的原点重合的点记作点A,数轴上的单位长度等于硬币的直径.将硬币沿数轴的正方向滚动以周,点A到达数轴上的点A′处,点A′对应的实数是π.
如图,将一枚硬币放到数轴上,把与数轴的原点重合的点记作点A,数轴上的单位长度等于硬币的直径.将硬币沿数轴的正方向滚动以周,点A到达数轴上的点A′处,点A′对应的实数是π.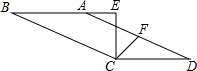 如图,已知?ABCD中,点F为AD的中点,CE⊥AB交BA的延长线于点E,连CF,若∠ECF=45°,试写出CD、AE、CE的数量关系,并证明你的猜想.
如图,已知?ABCD中,点F为AD的中点,CE⊥AB交BA的延长线于点E,连CF,若∠ECF=45°,试写出CD、AE、CE的数量关系,并证明你的猜想.