题目内容
8.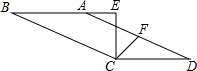 如图,已知?ABCD中,点F为AD的中点,CE⊥AB交BA的延长线于点E,连CF,若∠ECF=45°,试写出CD、AE、CE的数量关系,并证明你的猜想.
如图,已知?ABCD中,点F为AD的中点,CE⊥AB交BA的延长线于点E,连CF,若∠ECF=45°,试写出CD、AE、CE的数量关系,并证明你的猜想.
分析 延长BA,交CF延长线于G根据平行四边形的性质得到AB∥CD由平行线的性质得到∠GAF=∠D,∠G=∠GCD,推出△AGF≌△DCF,根据全等三角形的性质得到AG=CD,得到△CEG是等腰直角三角形,由等腰直角三角形的性质得到CE=EG,即可得到结论.
解答 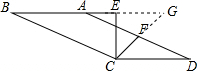 解:CD-AE=CE,
解:CD-AE=CE,
延长BA,交CF延长线于G
∵四边形ABCD是平行四边形
∴AB∥CD
∴∠GAF=∠D,∠G=∠GCD,
∵F是AD的中点,即AF=DF,
在△AGF与△DCF中,$\left\{\begin{array}{l}{∠GAF=∠D}\\{∠G=∠FCD}\\{AF=DF}\end{array}\right.$,
∴△AGF≌△DCF,
∴AG=CD,
∵CE⊥AB,∠ECF=45°,
∴△CEG是等腰直角三角形,
∴CE=EG,
∵EG=AG-AE=CD-AE
∴CD-AE=CE.
点评 本题考查了平行四边形的性质,全等三角形的判定和性质,等腰直角三角形的性质,平行线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知抛物线y=x2+4x+3的顶点为A,抛物线与x轴相交于点B和点C(点B在点C的左侧),与y轴相交于点D、点P为对称轴直线l上的一个动点,以每秒1个单位长度的速度从抛物线的顶点A向上运动.设点P运动的时间为t秒.
如图,已知抛物线y=x2+4x+3的顶点为A,抛物线与x轴相交于点B和点C(点B在点C的左侧),与y轴相交于点D、点P为对称轴直线l上的一个动点,以每秒1个单位长度的速度从抛物线的顶点A向上运动.设点P运动的时间为t秒.
 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是菱形ABCD各边的中点,求证:OE=OF=OG=0H.
已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是菱形ABCD各边的中点,求证:OE=OF=OG=0H.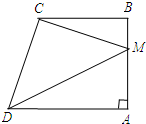 如图,四边形ABCD中,AD∥BC,∠BAD=90°,点M为AB上一点,连结CM,DM.
如图,四边形ABCD中,AD∥BC,∠BAD=90°,点M为AB上一点,连结CM,DM.