Question

如图，△ABC与△ADE都是以A为直角顶点的等腰直角三角形，DE交AC于点F，且AB=5，AD=3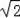．当△CEF是直角三角形时，BD=　　．

Answer 1

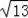
或1【考点】勾股定理；全等三角形的判定与性质；等腰直角三角形．

【分析】根据等腰直角三角形的性质可得AB=AC，AD=AE，再求出∠BAD=∠CAE，然后利用“边角边”证明△ABD和△ACE全等，根据全等三角形对应边相等可得BD=CE，再分①∠CFE=90°时，根据等腰直角三角形的性质可得AF=EF=AE，再求出CF的长，然后利用勾股定理列式求出CE，从而得解；②∠CEF=90°，求出∠AEC=135°，根据全等三角形对应角相等可得∠ADB=135°，然后求出点B、D、F三点共线，过点A作AG⊥DE，根据等腰直角三角形的性质求出AG=DG=AD，再利用勾股定理列式求出BG，然后根据BD=BG﹣DG计算即可得解．

【解答】解：∵△ABC与△ADE都是等腰直角三角形，

∴AB=AC，AD=AE，

∵∠BAD=∠BAC﹣∠CAD=90°﹣∠CAD，

∠CAE=∠DAE﹣∠CAD=90°﹣∠CAD，

∴∠BAD=∠CAE，

在△ABD和△ACE中，

，

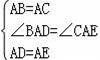
∴△ABD≌△ACE（SAS），

∴BD=CE，

①如图1，∠CFE=90°时，AF⊥DE，

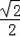
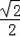
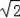
∴AF=EF=AE=×3=3，

CF=AC﹣AF=5﹣3=2，

在Rt△CEF中，CE===，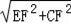

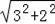
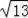
∴BD=CE=；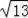

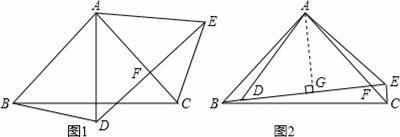
②如图2，∠CEF=90°时，∠AEC=135°，

∵△ABD≌△ACE，

∴∠ADB=∠AEC=135°，

∵∠ADB+∠ADE=135°+45°=180°，

∴点B、D、F三点共线，

过点A作AG⊥DE，

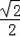
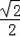
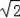
则AG=DG=AD=×3=3，

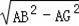
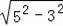
在Rt△ADG中，BG===4，

∴BD=BG﹣DG=4﹣3=1，

综上所述，BD=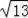或1．

故答案为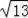：或1．