��Ŀ����
һ�������ĺ���װ�����ɸ�ֻ����ɫ��ͬ�ĺ��������
��1����������2�������2����������������������ǡ����һ��һ�ĸ����Ƕ��٣����û���״ͼ���б��ķ�ʽ˵����
��2�����ȴӺ�������8�����ϼǺŷŻغ��У��ٽ�������ʵ�飮����ʵ���Ҫ��ÿ������ǰ�Ƚ�����ȣ�����һ����¼��ɫ��Żغ��У��ټ�����һ������50�Σ�ͳ�ƽ�����±���
| �����ɫ | �Ǻ� | �мǺ� | ||
| ��ɫ | ��ɫ | ��ɫ | ��ɫ | |
| �����Ĵ��� | 18 | 28 | 2 | 2 |
������������ʵ��Ľ���ɹ�����к������ռ�������İٷ�֮����
��3���ڣ�2���������¹�����к���ĸ�����
�����㡿�б�������״ͼ��������Ƶ�ʹ��Ƹ��ʣ�
����������1�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ���������������������ǡ����һ��һ������������ø��ʹ�ʽ������ô𰸣�
��2�����������50������ʵ���У����ֺ���20�Σ�����30�Σ��̶���ô𰸣�
��3���������֪��50������ʵ���У������мǺŵ���4�Σ��������������̶���ô𰸣�
����𡿽⣺��1������״ͼ�ã�
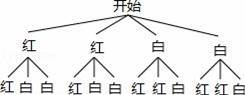

�߹���12�ֵȿ��ܵĽ����������������������ǡ����һ��һ����8�������
��P��ǡ����һ��һ�ף�=
 =
=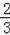
 ��
��
��2���������֪��50������ʵ���У����ֺ���20�Σ�����30�Σ�
�������ռ�ٷֱ�Ϊ20��50=40%��
������ռ�ٷֱ�Ϊ30��50=60%��
�𣺺���ռ40%������ռ60%��
��3���������֪��50������ʵ���У������мǺŵ���4�Σ�
��������Ϊ8��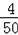
 =100��
=100��
�������Ϊ100��40%=40��
�𣺺��к�����40����
��

 �Ľ�Ϊ
�Ľ�Ϊ ����
����

 ��t��ֵ��
��t��ֵ�� S��ABC�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
S��ABC�������ڣ������t��ֵ���������ڣ���˵�����ɣ�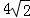 ��������AECD��
��������AECD��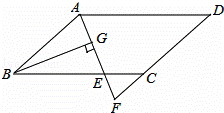



 =0��������߳�Ϊ��
=0��������߳�Ϊ��
