题目内容
某花店计划用100个花盆培育一种花卉,用于国庆销售.已知花店从批发市场购进花苗的单价y(元)和数量x(百株)之间的关系式是y=-x+14(其中6≤x≤13).根据以往经验,每年的花卉供不应求,但若每个花盆培育6株,每株的销售单价为26元,每个花盆每增加一株,每株的销售单价就减少2元.
(1)若要使每个花盆的销售总额P(元)最高,每个花盆应该培育多少花卉?
(2)若要使花店的总利润W(元)最大,每盆又应该培育多少株花卉?最大利润是多少?
(1)若要使每个花盆的销售总额P(元)最高,每个花盆应该培育多少花卉?
(2)若要使花店的总利润W(元)最大,每盆又应该培育多少株花卉?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)设每个花盆应该培育a株花卉,则每株花卉的售价为:[26-2(a-6)]元,由数量×单价=总价建立p与a的关系式即可;
(2)根据(1)结论分别求出求出每株的进价,由利润=销售总额-进价总额就可以得出结论.
(2)根据(1)结论分别求出求出每株的进价,由利润=销售总额-进价总额就可以得出结论.
解答:解:(1)设每个花盆应该培育a株花卉,则每株花卉的售价为:[26-2(a-6)]元,由题意,得
p=a[26-2(a-6)],
=-2(a-9.5)2+
,
∵a为整数,
∴a=9或10时,p最大=180.
答:每个花盆应该培育9株或10株花卉;
(2)每个花盆培育a株,100个花盆共100a,
∴y=-a+14.
∴W=[26-2(a-6)-(-a+14)]×100a=-100a2+2400a=-100(a-12)2+14400,
∴每盆应该培育12株花卉,最大利润是14400元.
p=a[26-2(a-6)],
=-2(a-9.5)2+
| 361 |
| 2 |
∵a为整数,
∴a=9或10时,p最大=180.
答:每个花盆应该培育9株或10株花卉;
(2)每个花盆培育a株,100个花盆共100a,
∴y=-a+14.
∴W=[26-2(a-6)-(-a+14)]×100a=-100a2+2400a=-100(a-12)2+14400,
∴每盆应该培育12株花卉,最大利润是14400元.
点评:本题考查了二次函数的解析式的运用,二次函数的性质的运用,利润率问题的数量关系的运用,解答时求出二次函数的关系式是关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
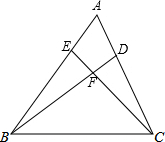 在△ABC中,D、E分别在AC、AB上,且满足∠ABD=∠ACE.
在△ABC中,D、E分别在AC、AB上,且满足∠ABD=∠ACE. 如图,点E是△ABC的内心,AE交△ABC的外接圆于点D,求证:BD=ED=CD.
如图,点E是△ABC的内心,AE交△ABC的外接圆于点D,求证:BD=ED=CD. 如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.
如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.