题目内容
已知x2+y2+2x-8y+17=0，求x2005+xy的值．
考点：配方法的应用,非负数的性质：偶次方
专题：计算题
分析：已知等式变形后，利用完全平方公式化简，再利用非负数的性质求出x与y的值，即可确定出原式的值．
解答：解：∵x2+y2+2x-8y+17=（x+1）2+（y-4）2=0，
∴x=-1，y=4，
则原式=-1-4=-5．
∴x=-1，y=4，
则原式=-1-4=-5．
点评：此题考查了配方法的应用，以及非负数的性质，熟练掌握运算法则是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，CA、CD分别与⊙O相切于A、D，AB为⊙O的直径，CO的延长线交⊙O于E，求证：∠B=2∠BDE．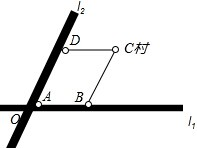
如图所示，两条笔直的公路l1、l2相交于点O，村庄C的村民在公路的旁边建三个加工厂A、B、D，已知AD=AB=6km，CD=CB=5km，村庄C到公路l1的距离为4km，则村庄C到公路l2的距离是
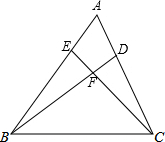在△ABC中，D、E分别在AC、AB上，且满足∠ABD=∠ACE．
如图，已知：过△ABC的底边BC的中点D任作一条直线交AC于点Q，交AB的延长线于点P，作AE∥BC交DQ的延长线于点E．求证：PD•QE=DQ•PE．