题目内容
一个钢筋三角架三边长分别是30厘米、75厘米、90厘米,现在再做一个与其相似的钢筋三角架,而只有长为45厘米和75厘米的两根钢筋,要求以其中一根为一边,从另一根上截下两段(允许有余料)作为两边,则不同的截法有多少种?写出你的设计方案,并说明理由.
考点:相似三角形的应用
专题:
分析:设截成的两边的长分别为xcm、ycm,然后根据相似三角形对应边成比例,分45cm与三角架的三边是对应边三种情况讨论求解,再根据两边之和不大于75cm解答.
解答:解:设截成的两边的长分别为xcm、ycm,
①45cm与30cm是对应边时,
新做三角架的两边之和一定大于75cm,不符合;
②45cm与75cm是对应边时,
∵两三角架相似,
∴
=
=
,
解得x=18,y=54,
∵18+54=72cm<75cm,
∴从75cm长的钢筋截取18cm和54cm两根;
③45cm与90cm是对应边时,
∵两三角架相似,
∴
=
=
,
解得x=15,y=37.5,
∵15+37.5=52.5cm<75cm,
∴从75cm长的钢筋截取15cm和37.5cm两根;
综上所述,共有两种截法:方法一:从75cm长的钢筋截取18cm和54cm两根,
方法二:从75cm长的钢筋截取15cm和37.5cm两根.
①45cm与30cm是对应边时,
新做三角架的两边之和一定大于75cm,不符合;
②45cm与75cm是对应边时,
∵两三角架相似,
∴
| 45 |
| 75 |
| x |
| 30 |
| y |
| 90 |
解得x=18,y=54,
∵18+54=72cm<75cm,
∴从75cm长的钢筋截取18cm和54cm两根;
③45cm与90cm是对应边时,
∵两三角架相似,
∴
| 45 |
| 90 |
| x |
| 30 |
| y |
| 75 |
解得x=15,y=37.5,
∵15+37.5=52.5cm<75cm,
∴从75cm长的钢筋截取15cm和37.5cm两根;
综上所述,共有两种截法:方法一:从75cm长的钢筋截取18cm和54cm两根,
方法二:从75cm长的钢筋截取15cm和37.5cm两根.
点评:本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,难点在于根据对应边的不同分情况讨论.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图所示,在⊙O中,AB是直径,BD是弦,半径OC∥BD,求证:
如图所示,在⊙O中,AB是直径,BD是弦,半径OC∥BD,求证:
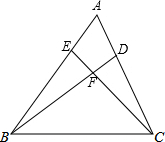 在△ABC中,D、E分别在AC、AB上,且满足∠ABD=∠ACE.
在△ABC中,D、E分别在AC、AB上,且满足∠ABD=∠ACE. 如图,已知:过△ABC的底边BC的中点D任作一条直线交AC于点Q,交AB的延长线于点P,作AE∥BC交DQ的延长线于点E.求证:PD•QE=DQ•PE.
如图,已知:过△ABC的底边BC的中点D任作一条直线交AC于点Q,交AB的延长线于点P,作AE∥BC交DQ的延长线于点E.求证:PD•QE=DQ•PE. 如图,点E是△ABC的内心,AE交△ABC的外接圆于点D,求证:BD=ED=CD.
如图,点E是△ABC的内心,AE交△ABC的外接圆于点D,求证:BD=ED=CD.