题目内容
20.为了测量一条河的高度,测量人员发现,该河两岸有一段是平行的,在河的一岸每隔4m有一棵树,在河的另一岸每隔40m有一根电线杆,你能想办法,测出河的宽度吗?测量人员是这样做的:他们发现,站在离有数的河岸30m处看对岸,看到对岸相邻的两根电线杆恰好被两棵树遮住,并且在这两棵树之间还有一棵树,利用相似三角形的知识计算河宽,请你帮助测量人员计算一下河宽.
分析 画出几何图形:如图,点P为观测点,CD=40m,AB=8m,作PF⊥CD于F,交AB于E,则PE=30m,证明△PAB∽△PCD,然后利用相似比计算出PF,再求出EF的长即可得到河的宽度.
解答 解: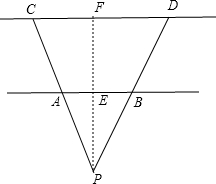 如图,点P为观测点,CD=40m,AB=8m,
如图,点P为观测点,CD=40m,AB=8m,
作PF⊥CD于F,交AB于E,则PE=30m,
∵AB∥CD,
∴△PAB∽△PCD,
∴$\frac{PE}{PF}$=$\frac{AB}{CD}$,即$\frac{30}{PF}$=$\frac{8}{40}$,
∴PF=150,
∴EF=PF-PE=150-30=120(m).
答:河宽为120m.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度;借助标杆或直尺测量物体的高度.找出几何图形上相应线段的长是解题的关键.

练习册系列答案
相关题目
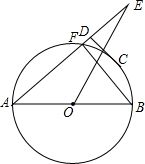 如图,⊙O的直径AB=8,点E在圆外,AE交⊙O于点F,C是圆心上一点,CD⊥AE于点D,AF=2CD=4$\sqrt{2}$.
如图,⊙O的直径AB=8,点E在圆外,AE交⊙O于点F,C是圆心上一点,CD⊥AE于点D,AF=2CD=4$\sqrt{2}$. 如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形,请你以图中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形,请你以图中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC. 如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=$\frac{1}{2}$AB,点E、F分别为AB、AD的中点,求△AEF与多边形BCDFE的面积之比.
如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=$\frac{1}{2}$AB,点E、F分别为AB、AD的中点,求△AEF与多边形BCDFE的面积之比.