题目内容
14.已知甲、乙两个班级各有50名学生.为了了解甲、乙两个班级学生解答选择题的能力状况,黄老师对某次考试中8道选择题的答题情况进行统计分析,得到统计表如下:| 人数(人) 答对的题数(道) 班级 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 甲班 | 0 | 1 | 1 | 3 | 4 | 11 | 16 | 12 | 2 |
| 乙班 | 0 | 1 | 0 | 2 | 5 | 12 | 15 | 13 | 2 |
(1)甲班学生答对的题数的众数是6;
(2)若答对的题数大于或等于7道的为优秀,则乙班该次考试中选择题答题的优秀率=30%(优秀率=$\frac{班级优秀人数}{班级总人数}$×100%).
(3)从甲、乙两班答题全对的学生中,随机抽取2人作选择题解题方法交流,画出树状图或列表求出抽到的2人在同一个班级的概率.
分析 (1)根据众数的定义,结合表格信息即可得出答案;
(2)先求出大于或等于7道的人数,继而根据优秀率=优秀人数÷总数即可得出答案;
(3)列出这两个人所在的班级情况,从而计算即可.
解答 解:(1)由表格可得,甲班答对6道题的人数最多,即甲班学生答对的题数的众数是6;
故答案为:6;
(2)乙班答对的题数大于或等于7道的人数有:13+2=15,
故优秀率为:$\frac{15}{50}$=30%;
(3)设甲班答题全对的两个人为A和B,乙班答题全对的两个人为C和D,
随机抽取2人的情况共有A和B、A和C、A和D、B和C、B和D、C和D共6种,
而抽到的2人在同一个班级的情况有A和B、C和D这2种,
故可得抽到的2人在同一个班级的概率=$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:6,30%,$\frac{1}{3}$.
点评 本题考查了众数、统计表及树状图求概率的知识,解答本题的关键是能准确读图,从表格中得到解题需要的信息,难度一般

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
4. 已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
(1)填空:a=-3,b=3,c=4;
(2)画出三角形ABC和三角形A′B′C′.
 已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:| 三角形ABC | A(a,2) | B(-5,1) | C(-2,0) |
| 三角形A′B′C′ | A′(3,4) | B′(1,b) | C′(c,2) |
(2)画出三角形ABC和三角形A′B′C′.
2.下列化简正确的是( )
| A. | $\sqrt{\frac{2}{3}}$=$\frac{\sqrt{2}}{3}$ | B. | $\sqrt{40}$=5$\sqrt{8}$ | C. | $\sqrt{\frac{8}{9}}$=$\frac{4\sqrt{2}}{3}$ | D. | 8$\sqrt{\frac{3}{2}}$=4$\sqrt{6}$ |
9.线段CD是由线段AB平移得到的,点A(1,8)的对应点C(-3,0),则点B(4,7)的对应点D的坐标为( )
| A. | (-1,0) | B. | (6,9) | C. | (0,-1) | D. | (9,6) |
6.右图是某几何体的三视图,该几何体是( )


| A. | 圆柱 | B. | 正方体 | C. | 圆锥 | D. | 长方体 |
3.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号是奇数的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.下列各数中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\root{3}{2}$ | C. | $\sqrt{4}$ | D. | $\sqrt{12}$ |
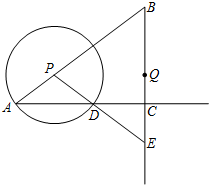 如图,在Rt∠ABC中,∠ACB=90°,AC=8,tanB=$\frac{4}{3}$,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,点Q是线段BE的中点.
如图,在Rt∠ABC中,∠ACB=90°,AC=8,tanB=$\frac{4}{3}$,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,点Q是线段BE的中点.