题目内容
已知AD是等腰△ABC的腰BC上的高,∠DAB=40°,则△ABC的顶角度数是 .
考点:等腰三角形的性质
专题:
分析:由于BC为腰,则点B可为顶角的顶点,也可为底角的顶点,高AD可在三角形内部也可在三角形外部,故应分三种情况分析计算.
解答:解:由题意得,分三种情况:

(1)当点B为顶角的顶点时,且AD在三角形内部,∠B=90°-∠DAB=90°-40°=50°;
(2)当点B为顶角的顶点时,且AD在三角形外部,∠ABC=∠D+∠DAB=90°+∠40°=130°;
(3)当点C为顶角的顶点时,∠B=90°-∠DAB=90°-40°=50°,
∴∠ACB=180°-2∠B=180°-2×50°=80°.
故答案为:50°或130°或80°.

(1)当点B为顶角的顶点时,且AD在三角形内部,∠B=90°-∠DAB=90°-40°=50°;
(2)当点B为顶角的顶点时,且AD在三角形外部,∠ABC=∠D+∠DAB=90°+∠40°=130°;
(3)当点C为顶角的顶点时,∠B=90°-∠DAB=90°-40°=50°,
∴∠ACB=180°-2∠B=180°-2×50°=80°.
故答案为:50°或130°或80°.
点评:本题考查了等腰三角形的性质,三角形的内角和定理,直角三角形的性质.注意分类讨论是正确解答本题的关键.

练习册系列答案
相关题目
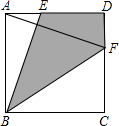 如图,E、F分别是正方形ABCD的边AD、DC上的点,BE⊥AF,若图中阴影部分的面积为8,则正方形的面积是( )
如图,E、F分别是正方形ABCD的边AD、DC上的点,BE⊥AF,若图中阴影部分的面积为8,则正方形的面积是( )| A、12 | B、16 | C、20 | D、24 |
若a>0,b<0,c<0,则方程ax2+bx+c=0的根的情况为( )
| A、有两个同号的实数根 |
| B、有两个异号的实数根,且负根的绝对值大 |
| C、有两个异号的实数根,且正根的绝对值大 |
| D、无实数根 |
 如图,梯形ABCD中,AB∥CD,AB=AC=AD,若∠BAD=140°,则∠B的度数为( )
如图,梯形ABCD中,AB∥CD,AB=AC=AD,若∠BAD=140°,则∠B的度数为( )| A、60° | B、70° |
| C、75° | D、80° |