题目内容
14.化简:(1)$\sqrt{12}-\sqrt{75}-\sqrt{48}$
(2)$\frac{{\sqrt{32}-\sqrt{8}}}{{\sqrt{2}}}$
(3)$3\sqrt{40}-5\sqrt{\frac{1}{10}}+2\sqrt{10}$
(4)$(\sqrt{5}-\sqrt{7})(\sqrt{5}+\sqrt{7})-{(2\sqrt{3}+1)^2}$.
分析 (1)先进行二次根式的化简,然后合并;
(2)先进行二次根式的化简,然后进行除法运算;
(3)先进行二次根式的化简,然后合并;
(4)先进行平方差公式和完全平方公式的运算,然后合并.
解答 解;(1)原式=2$\sqrt{3}$-5$\sqrt{3}$-4$\sqrt{3}$
=-7$\sqrt{3}$;
(2)原式=$\frac{4\sqrt{2}-2\sqrt{2}}{\sqrt{2}}$
=2;
(3)原式=4$\sqrt{10}$-$\frac{\sqrt{10}}{2}$+2$\sqrt{10}$
=$\frac{11}{2}$$\sqrt{10}$;
(4)原式=5-7-(12+4$\sqrt{3}$+1)
=-15-4$\sqrt{3}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简以及合并.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
9.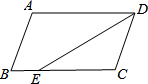 如图,在?ABCD中,已知AD=12cm,AB=8cm,DE平分∠ADC交BC边于点E,则BE等于( )
如图,在?ABCD中,已知AD=12cm,AB=8cm,DE平分∠ADC交BC边于点E,则BE等于( )
 如图,在?ABCD中,已知AD=12cm,AB=8cm,DE平分∠ADC交BC边于点E,则BE等于( )
如图,在?ABCD中,已知AD=12cm,AB=8cm,DE平分∠ADC交BC边于点E,则BE等于( )| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
6.下列关于$\sqrt{2}$的说法中,错误的是( )
| A. | $\sqrt{2}$是无理数 | B. | 1<$\sqrt{2}$<2 | ||
| C. | $\sqrt{2}$是2的算术平方根 | D. | 2的平方根是$\sqrt{2}$ |
3.如果规定“※”为一种运算符号,且a※b=ab-ba,则4※(2※1)的值为 ( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图所示,在△ABC中,已知∠A=90°,BD平分∠ABC,AD=6cm,BC=15cm,求△BDC的面积.
如图所示,在△ABC中,已知∠A=90°,BD平分∠ABC,AD=6cm,BC=15cm,求△BDC的面积. 如图,画一个三角形,使它与△ABC相似,且相似比为1:2.
如图,画一个三角形,使它与△ABC相似,且相似比为1:2.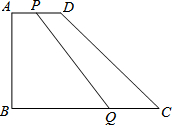 如图,在四边形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒.
如图,在四边形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒. 已知抛物线y=ax2+bx+3,经过点M(-4,0),且对称轴为x=-$\frac{5}{2}$,交y轴于B.
已知抛物线y=ax2+bx+3,经过点M(-4,0),且对称轴为x=-$\frac{5}{2}$,交y轴于B.