题目内容
17.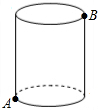 如图,有一圆柱,其高为8cm,它的底面半径为2cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为2$\sqrt{17}$ cm.(π取3)
如图,有一圆柱,其高为8cm,它的底面半径为2cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为2$\sqrt{17}$ cm.(π取3)
分析 先把圆柱的侧面展开得其侧面展开图,则A,B所在的长方形的长为圆柱的高12cm,宽为底面圆周长的一半为πr,蚂蚁经过的最短距离为连接A,B的线段长,由勾股定理求得AB的长.
解答 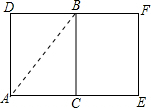 解:如图,将圆柱的侧面沿过A点的一条母线剪开,得到长方形ADFE,
解:如图,将圆柱的侧面沿过A点的一条母线剪开,得到长方形ADFE,
连接AB,则线段AB的长就是蚂蚁爬行的最短距离,其中C,B分别是AE,DF的中点.
∵AD=8cm,DB=πr=2π=6cm(π取3),
∴AB=$\sqrt{{AD}^{2}+{BD}^{2}}$=$\sqrt{{8}^{2}+{2}^{2}}$=2$\sqrt{17}$cm.
故答案为:2$\sqrt{17}$.
点评 本题考查的是平面展开-最短路径问题,根据题意画出圆柱的侧面展开图,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
12.下列各组数中是勾股数的一组是( )
| A. | 1,2,$\sqrt{5}$ | B. | 1,2,$\sqrt{3}$ | C. | 9,12,15 | D. | 6,8,12 |
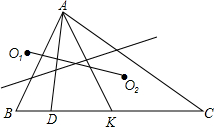 设D是△ABC的边BC上一点,但不是中点,设O1和O2分别是△ABD和△ADC的外心,求证:△ABC的中线AK的垂直平分线过线段O1O2中点.
设D是△ABC的边BC上一点,但不是中点,设O1和O2分别是△ABD和△ADC的外心,求证:△ABC的中线AK的垂直平分线过线段O1O2中点.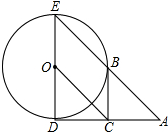 如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙0于点B,且BC∥ED.
如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙0于点B,且BC∥ED.