题目内容
4. 如图,在⊙O中,弦AB的长为8cm,OD⊥AB于C且CD=2cm,则⊙O的半径为5.
如图,在⊙O中,弦AB的长为8cm,OD⊥AB于C且CD=2cm,则⊙O的半径为5.
分析 先根据垂径定理求出AC的长,设⊙O的半径为r,再连接OA,在Rt△OAC中利用勾股定理求出r的值即可.
解答  解:∵⊙O的弦AB=8,半径OD⊥AB,
解:∵⊙O的弦AB=8,半径OD⊥AB,
∴AC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
设⊙O的半径为r,则OC=r-CD=r-2,连接OA,
在Rt△OAC中,
OA2=OC2+AC2,即r2=(r-2)2+42,解得r=5.
故答案为:5.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
14.已知x2-y2=4,x-y=2,则x+y等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
15.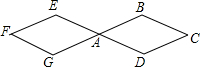 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )
 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )| A. | 点F | B. | 点G | C. | 点A | D. | 点C |
12.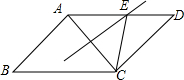 如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
 如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )| A. | 6 | B. | 8 | C. | 14 | D. | 16 |
19.下列图形中,旋转60°后可以和原图形重合的是( )
| A. | 正六边形 | B. | 正方形 | C. | 正五边形 | D. | 正三角形 |
13.方程x2-4x+4=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |