Question

3．如图，CD是⊙O的直径，点A是半圆上的三等分点，B是弧$\widehat{AD}$的中点，P点为直线CD上的一个动点，当CD=4时，AP+BP的最小值为2$\sqrt{2}$．

Answer 1

分析 本题是要在CD上找一点P，使PA+PB的值最小，设A′是A关于CD的对称点，连接A′B，与CD的交点即为点P．此时PA+PB=A′B是最小值，可证△OA′B是等腰直角三角形，从而得出结果．

解答 解：作点A关于CD的对称点A′，连接A′B，交CD于点P，则PA+PB最小，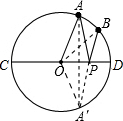
连接OA′，AA′．
∵点A与A′关于CD对称，点A是半圆上的一个三等分点，
∴∠A′OD=∠AOD=60°，PA=PA′，
∵点B是弧AD的中点，
∴∠BOD=30°，
∴∠A′OB=∠A′OD+∠BOD=90°，
又∵OA=OA′=2，
∴A′B=2$\sqrt{2}$．
∴PA+PB=PA′+PB=A′B=2$\sqrt{2}$．
故答案为：2$\sqrt{2}$．

点评 此题主要考查了轴对称最短线段问题以及垂径定理和勾股定理等知识，正确确定P点的位置是解题的关键，确定点P的位置这类题在课本中有原题，因此加强课本题目的训练至关重要．