题目内容
6.在△ABC中,∠C=90°,tanA=$\frac{1}{3}$,那么sinA的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 根据正切函数的定义,可得BC,AC的关系,根据勾股定理,可得AB的长,根据正弦函数的定义,可得答案.
解答 解:tanA=$\frac{BC}{AC}$=$\frac{1}{3}$,BC=x,AC=3x,
由勾股定理,得
AB=$\sqrt{10}$x,
sinA=$\frac{BC}{AB}$=$\frac{\sqrt{10}}{10}$,
故选:B.
点评 本题考查了同角三角函数的关系,利用正切函数的定义得出BC=x,AC=3x是解题关键.

练习册系列答案
相关题目
18.下列事件中属于不可能确定事件的是( )
| A. | 在足球赛中,弱队战胜强队 | |
| B. | 长分别为3、5、9厘米的三条线段能围成一个三角形 | |
| C. | 抛掷一枚硬币,落地后正面朝上 | |
| D. | 任取两个正整数,其和大于1 |
15.二次函数y=(x-1)2+3的顶点坐标为( )
| A. | (1,3) | B. | (-1,3) | C. | (1,-3) | D. | (-1,-3) |
 如图,抛物线y1=ax2+bx+c与直线y2=kx+n的图象交于A(-4,-1),B两点,下列判断中:①abc>0;②a+b+c<0;③不等式ax2+bx+c<kx+n的解集为-4<x<$\frac{1}{2}$;④方程ax2+bx+c=-1的解为x=-4,其中正确的个数是( )
如图,抛物线y1=ax2+bx+c与直线y2=kx+n的图象交于A(-4,-1),B两点,下列判断中:①abc>0;②a+b+c<0;③不等式ax2+bx+c<kx+n的解集为-4<x<$\frac{1}{2}$;④方程ax2+bx+c=-1的解为x=-4,其中正确的个数是( )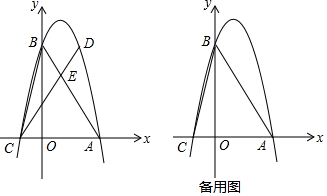
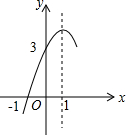 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: