题目内容
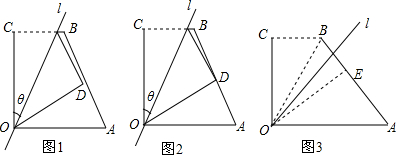
如图1,四边形OABC中,OA=a,OC=3,BC=2,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与
OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).
(1)若折叠后点D恰为AB的中点(如图2),则θ= ;
(2)若θ=45°,四边形OABC的直角∠OCB沿直线l折叠后,点B落在点四边形OABC的边AB上的E处(如图3),求a的值.
OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).
(1)若折叠后点D恰为AB的中点(如图2),则θ=
(2)若θ=45°,四边形OABC的直角∠OCB沿直线l折叠后,点B落在点四边形OABC的边AB上的E处(如图3),求a的值.

考点:翻折变换(折叠问题)
专题:计算题
分析:(1)延长ND交OA的延长线于M,根据折叠性质得∠CON=∠DON=θ,∠ODN=∠C=90°,由点D为AB的中点得到D点为MN的中点,所以OD垂直平分MN,则OM=ON,根据等腰三角形的性质得∠MOD=∠NOD=θ,则∠θ+∠θ+∠θ=90°,计算得到∠θ=30°;
(2)作ED⊥OA于D,根据折叠性质得AB⊥直线l,OD=OC=3,DE=BC=2,由于θ=45°,AB⊥直线l,即直线l平分∠AOC,则∠A=45°,所以△ADE为等腰直角三角形,则AD=DE=2,所以OA=OD+AD=3+2=5,即a=5.
(2)作ED⊥OA于D,根据折叠性质得AB⊥直线l,OD=OC=3,DE=BC=2,由于θ=45°,AB⊥直线l,即直线l平分∠AOC,则∠A=45°,所以△ADE为等腰直角三角形,则AD=DE=2,所以OA=OD+AD=3+2=5,即a=5.
解答: 解:(1)如图2,延长ND交OA的延长线于M,
解:(1)如图2,延长ND交OA的延长线于M,
∵四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,
∴∠CON=∠DON=θ,∠ODN=∠C=90°,
∵点D为AB的中点,
∴D点为MN的中点,
∴OD垂直平分MN,
∴OM=ON,
∴∠MOD=∠NOD=θ,
∴∠θ+∠θ+∠θ=90°,
∴∠θ=30°;
故答案为30°;
(2)如图3,作ED⊥OA于D,
∵四边形OABC的直角∠OCB沿直线l折叠后,点B落在点四边形OABC的边AB上的E处,
∴AB⊥直线l,OD=OC=3,DE=BC=2,
∵θ=45°,AB⊥直线l,
即直线l平分∠AOC,
∴∠A=45°,
∴△ADE为等腰直角三角形,
∴AD=DE=2,
∴OA=OD+AD=3+2=5,
∴a=5.
 解:(1)如图2,延长ND交OA的延长线于M,
解:(1)如图2,延长ND交OA的延长线于M,∵四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,
∴∠CON=∠DON=θ,∠ODN=∠C=90°,
∵点D为AB的中点,
∴D点为MN的中点,
∴OD垂直平分MN,
∴OM=ON,
∴∠MOD=∠NOD=θ,
∴∠θ+∠θ+∠θ=90°,
∴∠θ=30°;
故答案为30°;
(2)如图3,作ED⊥OA于D,
∵四边形OABC的直角∠OCB沿直线l折叠后,点B落在点四边形OABC的边AB上的E处,
∴AB⊥直线l,OD=OC=3,DE=BC=2,
∵θ=45°,AB⊥直线l,
即直线l平分∠AOC,
∴∠A=45°,
∴△ADE为等腰直角三角形,
∴AD=DE=2,
∴OA=OD+AD=3+2=5,
∴a=5.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了线段垂直平分线的性质.

练习册系列答案
相关题目
下列变形中,正确的是( )
A、(2
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列说法:①相反数等于本身的数是0;②绝对值等于本身的是正数;③倒数等于本身的数是±1; ④平方等于本身的数是0和1;⑤平方为9的数是3;⑥有绝对值最小的有理数.正确的个数为( )
| A、1 | B、2 | C、3 | D、4 |
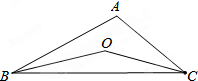 如图,BO、CO分别平分∠ABC和∠ACB.若∠A=100°,则∠O的度数=( )
如图,BO、CO分别平分∠ABC和∠ACB.若∠A=100°,则∠O的度数=( )| A、130° | B、135° |
| C、140° | D、120° |
 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积的积为( )
如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积的积为( )A、(
| ||
B、
| ||
C、
| ||
D、(
|
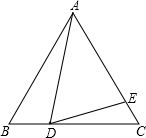 如图所示,△ABC是等边三角形,AB=6,D、E分别为BC、AC上一点,∠ADE=60°.
如图所示,△ABC是等边三角形,AB=6,D、E分别为BC、AC上一点,∠ADE=60°.