Question

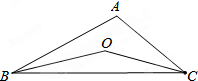如图，BO、CO分别平分∠ABC和∠ACB．若∠A=100°，则∠O的度数=（　　）

• A、130°
• B、135°
• C、140°
• D、120°

Answer 1

考点：三角形内角和定理

专题：

分析：先根据角平分线的定义得到∠OBC=

1

2

∠ABC，∠OCB=

1

2

∠ACB，再根据三角形内角和定理得到∠BOC=180°-（∠OBC+∠OCB），∠ABC+∠ACB=180°-∠A，则∠BOC=180°-

1

2

（180°-∠A）=90°+

1

2

∠A，然后把∠A的度数代入计算即可．

解答：解：∵BO、CO分别平分∠ABC和∠ACB，
∴∠OBC=

1

2

∠ABC，∠OCB=

1

2

∠ACB，
∵∠BOC=180°-（∠OBC+∠OCB），
∴∠BOC=180°-

1

2

（∠ABC+∠ACB），
∵∠ABC+∠ACB=180°-∠A，
∴∠BOC=180°-

1

2

（180°-∠A）
=90°+

1

2

∠A，
而∠A=100°，
∴∠BOC=90°+50°=140°．
故选C．

点评：本题考查了三角形内角和定理：三角形内角和是180°．