题目内容
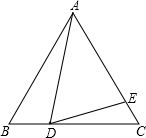 如图所示,△ABC是等边三角形,AB=6,D、E分别为BC、AC上一点,∠ADE=60°.
如图所示,△ABC是等边三角形,AB=6,D、E分别为BC、AC上一点,∠ADE=60°.(1)求证:△ABD∽△DCE;
(2)设BD=x,CE=y,求y与x的函数表达式.
考点:相似三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)根据等边三角形的性质得∠B=∠C=60°,再根据三角形外角性质得∠ADE+∠EDC=∠B+∠BAD,而∠ADE=60°,所以∠EDC=∠BAD,于是可判断△ABD∽△DCE;
(2)根据等边三角形三角形性质得BC=AB=6,再由△ABD∽△DCE,然后利用相似比得到
=
,然后整理即可.
(2)根据等边三角形三角形性质得BC=AB=6,再由△ABD∽△DCE,然后利用相似比得到
| 6 |
| 6-x |
| x |
| y |
解答:(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠ADC=∠B+∠BAD,即∠ADE+∠EDC=∠B+∠BAD,
而∠ADE=60°,
∴∠EDC=∠BAD,
∴△ABD∽△DCE;
(2)解:∵△ABC是等边三角形,
∴BC=AB=6
∵BD=x,
∴DC=6-x,
∵△ABD∽△DCE,
∴
=
,即
=
,
∴y=-
x2+x(0<x<6).
∴∠B=∠C=60°,
∵∠ADC=∠B+∠BAD,即∠ADE+∠EDC=∠B+∠BAD,
而∠ADE=60°,
∴∠EDC=∠BAD,
∴△ABD∽△DCE;
(2)解:∵△ABC是等边三角形,
∴BC=AB=6
∵BD=x,
∴DC=6-x,
∵△ABD∽△DCE,
∴
| AB |
| DC |
| BD |
| CE |
| 6 |
| 6-x |
| x |
| y |
∴y=-
| 1 |
| 6 |
点评:本题考查了相似三角形的判定与性质:有两组角对应相等的三角形相似;相似三角形对应边的比相等,都等于相似比.也考查了等边三角形的性质.

练习册系列答案
相关题目
一个等腰三角形的一个外角等于100°,则这个等腰三角形的底角为( )
| A、55° |
| B、70° |
| C、55°或40° |
| D、80°或50° |
一组对边平行,并且对角线互相垂直且相等的四边形是( )
| A、菱形 | B、正方形 |
| C、矩形 | D、平行四边形 |
若方程x2-4x+c=0有两个相等的实数根,则实数c的值是( )
| A、6 | B、5 | C、4 | D、3 |
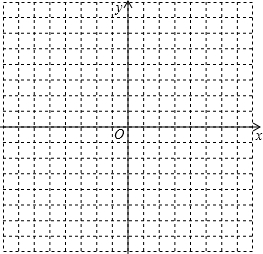 建立直角坐标系,标出以下各组点,并将各组内的点用线段依次连接起来,观察所得的图形,你认为它是什么?
建立直角坐标系,标出以下各组点,并将各组内的点用线段依次连接起来,观察所得的图形,你认为它是什么?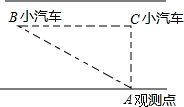 “交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米C处,过了2秒后,测得小汽车在B处与车速检测仪间距离为50米,这辆小汽车超速了吗?
“交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米C处,过了2秒后,测得小汽车在B处与车速检测仪间距离为50米,这辆小汽车超速了吗?