��Ŀ����
4���Ķ����⣺����һ�����ڶ�������ʽx2+2ax+a2����ֱ���ù�ʽ���ֽ�Ϊ��x+a��2����ʽ�������ڶ�������ʽx4-3x2+1���Ͳ���ֱ���ù�ʽ���ˣ����ǿ��Ѷ�������ʽx4-3x2+1��3x2���2x2+x2������
��x4-3x2+1=x4-2x2-x2+1=x4-2x2+1-x2=��x2-1��2-x2=��x2-x-1����x2+x-1����
�����������Ѷ�������ʽ�ֽ���ʽ�ķ����в����
��1���������������Զ���x4-7x2+9������ʽ�ֽ⣻
���϶�����һ����ʽд��������ʽ�ĺͽ����������ʽ��ʾ�ɲ��ַ�ʽ����ν�$\frac{1-3x}{{x}^{2}-1}$��ʾ�ɲ��ַ�ʽ��
���ʽ$\frac{1-3x}{{x}^{2}-1}$=$\frac{m}{x-1}$$+\frac{n}{x+1}$������ʽ���ұ�ͨ�ֵã�$\frac{m��x+1��+n��x-1��}{��x+1����x-1��}$=$\frac{��m+n��x+m-n}{��x+1����x-1��}$
��$\frac{1-3x}{{x}^{2}-1}$=$\frac{��m+n��x+m-n}{��x-1����x+1��}$��$\left\{\begin{array}{l}{m+n=-3}\\{m-n=1}\end{array}\right.$���$\left\{\begin{array}{l}{m=-1}\\{n=-2}\end{array}\right.$������$\frac{1-3x}{{x}^{2}-1}$=$\frac{-1}{x-1}$$+\frac{-2}{x+1}$��
��2������������������ʽ$\frac{4x-3}{��2x+1����x-2��}$д�ɲ��ַ�ʽ�ĺ͵���ʽ��
���� ��1�����ò��������ʽ�ֽ⼴�ɣ�
��2�����ݲ��϶��ṩ�Ľ��ⲽ���뷽�����н��
��� �⣺��1��x4-7x2+9��
=x4-6x2+9-x2��
=��x2-3��2-x2��
=��x2-3+x����x2-3-x����
��2�����ʽ$\frac{4x-3}{��2x+1����x-2��}$=$\frac{m}{2x+1}$-$\frac{n}{x-2}$��
����ʽ���ұ�ͨ�ֵã�$\frac{m��x-2��-n��2x+1��}{��2x+1����x-2��}$=$\frac{��m-2n��x-��2m+n��}{��2x+1����x-2��}$��
��$\frac{4x-3}{��2x+1����x-2��}$=$\frac{��m-2n��x-��2m+n��}{��2x+1����x-2��}$��$\left\{\begin{array}{l}{m-2n=4}\\{2m+n=3}\end{array}\right.$��
���$\left\{\begin{array}{l}{m=2}\\{n=-1}\end{array}\right.$��
����$\frac{4x-3}{��2x+1����x-2��}$=$\frac{2}{2x+1}$+$\frac{1}{x-2}$��
���� ���⿼������ʽ�ֽ��Ӧ�ã���Ϥ�����ṩ�Ľ��ⷽ���Ͳ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
19������ʽ$\left\{\begin{array}{l}{2x-1��-3}\\{4-\frac{1}{3}x��2}\end{array}\right.$�Ľ⼯�ǣ�������
| A�� | x��6 | B�� | -1��x��6 | C�� | -1��x��6 | D�� | x��-1 |
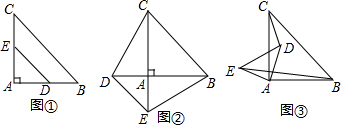
 ��ͼ����D��E�ֱ��ڡ�ABC��BC��AC�ϣ������߶�AD��BE���ڵ�F����AE��EC=1��3��BD��DC=2��3����EF��FB=$\frac{3}{8}$��
��ͼ����D��E�ֱ��ڡ�ABC��BC��AC�ϣ������߶�AD��BE���ڵ�F����AE��EC=1��3��BD��DC=2��3����EF��FB=$\frac{3}{8}$��