题目内容
12．
如图1，若∠1=∠2，∠3=73°，则∠4=107．
分析 根据已知一对同位角相等，利用同位角相等两直线平行得到a与b平行，利用两直线平行同旁内角互补得到一对角互补，再利用对顶角相等即可确定出∠4的度数．
解答 
解：∵∠1=∠2，
∴a∥b，
∴∠5+∠3=180°，
∵∠4=∠5，∠3=73°，
∴∠4+∠3=180°，
则∠4=107°．
故答案为：107．
点评 此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．
练习册系列答案
相关题目
3．下列各式从左边到右边的变形是因式分解的是（ ）
| A． | （a+b）2-4（a+b）+4=（a+b-2）2 | B． | （y+5）（y-5）=y2-25 | ||
| C． | x2+2x+1=x（x+2）+1 | D． | -18x4y3=-6x2y2•3x2y |
7．已知四边形ABCD中，AC与BD交于点O，如果只给出条件“AB∥CD”，那么可以判定四边形ABCD是平行四边形的是（ ）
①再加上条件“BC=AD”，则四边形ABCD一定是平行四边形．
②再加上条件“∠BAD=∠BCD”，则四边形ABCD一定是平行四边形．
③再加上条件“AO=CO”，则四边形ABCD一定是平行四边形．
④再加上条件“∠DBA=∠CAB”，则四边形ABCD一定是平行四边形．
①再加上条件“BC=AD”，则四边形ABCD一定是平行四边形．
②再加上条件“∠BAD=∠BCD”，则四边形ABCD一定是平行四边形．
③再加上条件“AO=CO”，则四边形ABCD一定是平行四边形．
④再加上条件“∠DBA=∠CAB”，则四边形ABCD一定是平行四边形．
| A． | ①和② | B． | ①③和④ | C． | ②和③ | D． | ②③和④ |
17．下列各式正确的是（ ）
| A． | $\frac{n}{m}$=$\frac{n-a}{m-a}$ | B． | $\frac{y}{x}$=$\frac{{y}^{2}}{{x}^{2}}$ | C． | $\frac{a+x}{b+x}$=$\frac{a+1}{b+1}$ | D． | $\frac{n}{m}$=$\frac{na}{ma}$（a≠0） |
如图：∠CAB=∠DAE，要使△ABD≌△ACE，需加的两个条件是AB=AC，AD=AE．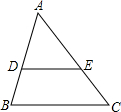
如图，已知$\frac{AD}{BD}$=$\frac{AE}{EC}$=$\frac{3}{2}$，试求$\frac{DE}{BC}$的值．