题目内容
(1)化简:(x4+x2+1)(x4-x2-1),x≠0;
(2)分解因式:7a2-3b+ab-21a;
(3)分解因式:9x2-24xy+16y2+6x-8y-3.
(2)分解因式:7a2-3b+ab-21a;
(3)分解因式:9x2-24xy+16y2+6x-8y-3.
考点:整式的混合运算,因式分解-分组分解法
专题:
分析:(1)利用平方差公式计算即可;
(2)分组提取公因式法分解因式即可;
(3)分组利用完全平方公式和提取公因式法分解因式即可.
(2)分组提取公因式法分解因式即可;
(3)分组利用完全平方公式和提取公因式法分解因式即可.
解答:解:(1)原式=[x4+(x2+1)][x4-(x2+1)]
=x8-(x2+1)2
=x8-x4-2x2-1;
(2)原式=7a2-21a-3b+ab
=7a(a-3)+b(a-3)
=(7a+b)(a-3);
(3)原式=(3x-4y)2+2(3x-4y)-3
=(3x-4y+3)(3x-4y-1).
=x8-(x2+1)2
=x8-x4-2x2-1;
(2)原式=7a2-21a-3b+ab
=7a(a-3)+b(a-3)
=(7a+b)(a-3);
(3)原式=(3x-4y)2+2(3x-4y)-3
=(3x-4y+3)(3x-4y-1).
点评:此题考查整式的混合运算和因式分解的灵活运用,掌握计算公式是解决问题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 找出全等图形.
找出全等图形. 已知AE是△ABC的BC边上的中线,O是AE的中点,连接BO并延长,交AC边于点D.求证:CD=2AD.
已知AE是△ABC的BC边上的中线,O是AE的中点,连接BO并延长,交AC边于点D.求证:CD=2AD.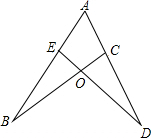 如图,已知AB=AD,BO=DO,求证:AE=AC.
如图,已知AB=AD,BO=DO,求证:AE=AC.