题目内容
5.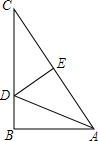 如图,Rt△ABC中,∠B=90°,AB=6,BC=8,现将△ABC翻折,使点C与点A重合,折痕为DE,求CD及DE的长.
如图,Rt△ABC中,∠B=90°,AB=6,BC=8,现将△ABC翻折,使点C与点A重合,折痕为DE,求CD及DE的长.
分析 先在RtABC中利用勾股定理计算出AB=10,再利用折叠的性质得到AD=CD,AE=CE=5,设CD=AD=x,则BD=8-x,在Rt△ABD中根据勾股定理可得到x2=62+(8-x)2,求得CD,进一步利用勾股定理求得DE即可.
解答 解:∵AB=6,AC=8,
∴BC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∵△ABC翻折,使点C与点A重合,折痕为DE,
∴AE=CE=5,AD=CD,
设CD=AD=x,
则BD=8-x,
在Rt△ABE中,
AB2+BD2=AD2
即:62+(8-x)2=x2
解得:x=$\frac{25}{4}$.
∴CD=$\frac{25}{4}$.
∴DE=$\sqrt{C{D}^{2}-C{E}^{2}}$=$\frac{5}{4}$.
点评 本题考查了折叠的性质:折叠前后两图象全等,即对应角相等,对应边相等.也考查了勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
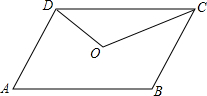 如图,O是?ABCD的对称中心,这个图形是不是中心对称图形?如果认为是,请说明理由;如果认为不是,在原图上添加一些线,使它成为中心对称图形.
如图,O是?ABCD的对称中心,这个图形是不是中心对称图形?如果认为是,请说明理由;如果认为不是,在原图上添加一些线,使它成为中心对称图形. 如图,⊙O的半径为4.
如图,⊙O的半径为4.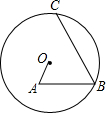 如图所示,在⊙O内有折线OABC,其中OA=4,AB=6,∠A=∠B=60°,则BC的长为10.
如图所示,在⊙O内有折线OABC,其中OA=4,AB=6,∠A=∠B=60°,则BC的长为10.