题目内容
17.化简:$\sqrt{(x+1)(-{x}^{2}+x+2)}$(x<-1)=(-x-1)$\sqrt{2-x}$.分析 根据因式分解,可得$\sqrt{(x+1)^{2}(2-x)}$,根据二次根式的性质,可得答案.
解答 解:∵x<-1,
∴x+1<0
原式=$\sqrt{(x+1)[(x+1)(-x+2)}$
=$\sqrt{(x+1)^{2}(2-x)}$
=|x+1|$\sqrt{2-x}$
=(-x-1)$\sqrt{2-x}$.
故答案为:(-x-1)$\sqrt{2-x}$.
点评 本题考查了二次根式的性质与化简,利用因式分解得出$\sqrt{(x+1)^{2}(2-x)}$是解题关键,又利用了二次根式的性质.

练习册系列答案
相关题目
2.下列各图是由若干盆花组成的形如正方形的图案,每条边上(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数是s,按图所示的图案回答下列问题.

(1)填表:
(2)当n=10时,s的值是多少?s是如何随n的变化而变化的?

(1)填表:
| n | 2 | 3 | 4 | 5 | 6 | … | n |
| s | 4 | 9 | 16 | 25 | 36 | … | n2 |
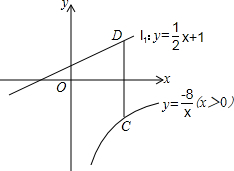 阅读理解:对于任意正实数a、b,∵${(\sqrt{a}-\sqrt{b})^2}$≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,只有当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵${(\sqrt{a}-\sqrt{b})^2}$≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,只有当a=b时,等号成立.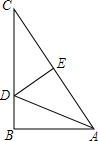 如图,Rt△ABC中,∠B=90°,AB=6,BC=8,现将△ABC翻折,使点C与点A重合,折痕为DE,求CD及DE的长.
如图,Rt△ABC中,∠B=90°,AB=6,BC=8,现将△ABC翻折,使点C与点A重合,折痕为DE,求CD及DE的长.
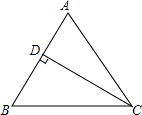 已知:如图△ABC中,AB=AC,CD⊥AB,D为垂足,且sin∠BCD=$\frac{5}{8}$.求:
已知:如图△ABC中,AB=AC,CD⊥AB,D为垂足,且sin∠BCD=$\frac{5}{8}$.求: