题目内容
14. 如图,⊙O的半径为4.
如图,⊙O的半径为4.(1)求作它的内接正方形ABCD;
(2)求正方形ABCD的边长.
分析 (1)把圆四等分,即可得出它的内接正方形ABCD;
(2)过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论
解答  解:(1)如图;
解:(1)如图;
(2)过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,
∴∠OBE=45°, ∴OE=BE,
∴OE=BE,
∵OE2+BE2=OB2,
∴2BE2=OB2=42=16,
∴BE=2$\sqrt{2}$,
∴BC=2BE=4$\sqrt{2}$,即正方形ABCD的边长是4$\sqrt{2}$.
点评 本题考查的是圆周角定理、垂径定理及勾股定理,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.

练习册系列答案
相关题目
4.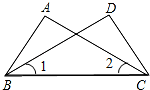 如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )
 如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )| A. | AB=DC | B. | AC=DB | C. | ∠1=∠2 | D. | ∠A=∠D |
2.下列各图是由若干盆花组成的形如正方形的图案,每条边上(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数是s,按图所示的图案回答下列问题.

(1)填表:
(2)当n=10时,s的值是多少?s是如何随n的变化而变化的?

(1)填表:
| n | 2 | 3 | 4 | 5 | 6 | … | n |
| s | 4 | 9 | 16 | 25 | 36 | … | n2 |
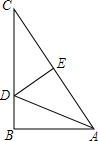 如图,Rt△ABC中,∠B=90°,AB=6,BC=8,现将△ABC翻折,使点C与点A重合,折痕为DE,求CD及DE的长.
如图,Rt△ABC中,∠B=90°,AB=6,BC=8,现将△ABC翻折,使点C与点A重合,折痕为DE,求CD及DE的长.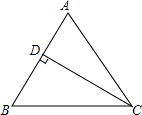 已知:如图△ABC中,AB=AC,CD⊥AB,D为垂足,且sin∠BCD=$\frac{5}{8}$.求:
已知:如图△ABC中,AB=AC,CD⊥AB,D为垂足,且sin∠BCD=$\frac{5}{8}$.求: 已知四个数:a=(-2)2,b=-|-2|,c=-(-1)2016,d=-(-3).
已知四个数:a=(-2)2,b=-|-2|,c=-(-1)2016,d=-(-3).