题目内容
14.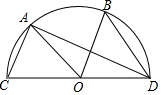 如图,CD是⊙O的直径,A,B两点在圆上,且AC∥OB,∠ADB=33°,则∠ADC的度数等于( )
如图,CD是⊙O的直径,A,B两点在圆上,且AC∥OB,∠ADB=33°,则∠ADC的度数等于( )| A. | 24° | B. | 28° | C. | 30° | D. | 33° |
分析 先根据圆周角定理得出∠DAC=90°,再由AC∥OB得出OB⊥AD,故$\widehat{AD}$=2$\widehat{AB}$,故可得出∠C的度数,根据直角三角形的性质即可得出结论.
解答 解:∵CD是⊙O的直径,
∴∠DAC=90°.
∵AC∥OB,∠ADB=33°,
∴OB⊥AD,
∴$\widehat{AD}$=2$\widehat{AB}$,
∴∠C=2∠ADB=66°,
∴∠ADC=90°-66°=24°.
故选A.
点评 本题考查的是圆周角定理,熟知直径所对的圆周角是直角是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.景德镇昌河汽车制造厂本周计划每日生产100辆北斗星小轿车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如表(增加的辆数为正数,减少的辆数为负数)
根据记录回答:
(1)本周生产了多少辆小轿车?
(2)本周总生产量与计划量相比是增加了还是减少了?增加或减少了多少辆?
(3)生产量最多的一天比生产量最少的一天多生产多少辆?
| 星 期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增 减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周生产了多少辆小轿车?
(2)本周总生产量与计划量相比是增加了还是减少了?增加或减少了多少辆?
(3)生产量最多的一天比生产量最少的一天多生产多少辆?
4.已知等腰三角形的周长为15cm,其中一边长为7cm,则底边长为( )
| A. | 4cm或7cm | B. | 1cm或7cm | C. | 4cm | D. | 7cm |
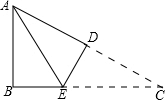 如图所示,在△ABC中,AB=5,BC=7,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为12.
如图所示,在△ABC中,AB=5,BC=7,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为12. 如图的数阵由若干个偶数排成.
如图的数阵由若干个偶数排成.