题目内容
6.已知抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4S△BOC,求点P的坐标.
分析 (1)根据点A、C的坐标利用待定系数法即可求出抛物线的解析式;
(2)根据二次函数的解析式利用二次函数图象上点的坐标特征求出点B的坐标,再结合S△AOP=4S△BOC即可得出关于x的含绝对值符号的一元二次方程,解方程求出x的值,由此即可得出点P的坐标.
解答 解:(1)把A(-3,0),C(0,3)代入y=-x2+bx+c,
得:$\left\{\begin{array}{l}{-9-3b+c=0}\\{c=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
∴该抛物线的函数表达式为y=-x2-2x+3.
(2)∵y=-x2-2x+3=-(x+3)(x-1),
∴点B(1,0).
设点P(x,-x2-2x+3),
∵S△AOP=4S△BOC,
∴$\frac{1}{2}$×3×|-x2-2x+3|=4×$\frac{1}{2}$×1×3,
整理,得:(x+1)2=0或x2+2x-7=0,
解得:x=-1或x=-1±$\sqrt{2}$,
∴点P的坐标为(-1,4)或(-1+$\sqrt{2}$,-4)或(-1-$\sqrt{2}$,-4).
点评 本题考查了待定系数法求二次函数的解析式以及二次函数图象上点的坐标特征,根据点的坐标利用待定系数法求出二次函数的解析式是解题的关键.

练习册系列答案
相关题目
14.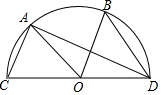 如图,CD是⊙O的直径,A,B两点在圆上,且AC∥OB,∠ADB=33°,则∠ADC的度数等于( )
如图,CD是⊙O的直径,A,B两点在圆上,且AC∥OB,∠ADB=33°,则∠ADC的度数等于( )
 如图,CD是⊙O的直径,A,B两点在圆上,且AC∥OB,∠ADB=33°,则∠ADC的度数等于( )
如图,CD是⊙O的直径,A,B两点在圆上,且AC∥OB,∠ADB=33°,则∠ADC的度数等于( )| A. | 24° | B. | 28° | C. | 30° | D. | 33° |
18.填在如图各正方形中的四个数之间都有一定的规律,按此规律得出a、b的值分别为( )
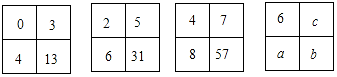

| A. | 10、91 | B. | 12、91 | C. | 10、95 | D. | 12、95 |
16.下列各组算式中,结果为负数的是( )
| A. | -(-1) | B. | (-1)2 | C. | (-3)×(-5) | D. | -|-1| |
 小敏在作⊙O的内接正五边形时.先做了如下几个步骤:
小敏在作⊙O的内接正五边形时.先做了如下几个步骤: