题目内容
 已知:如图,在?ABCD中,点E在BC边上,连接AE. O为AE中点,连接BO并延长交AD于F.
已知:如图,在?ABCD中,点E在BC边上,连接AE. O为AE中点,连接BO并延长交AD于F.(1)求证:△AOF≌△EOB,
(2)判断当AE平分∠BAD时,四边形ABEF是什么特殊四边形,并证明你的结论.
(3)当∠ABC=
考点:等腰梯形的判定,全等三角形的判定与性质,平行四边形的性质
专题:
分析:(1)先由平行四边形的性质得出AD∥BC,再根据平行线的性质得出∠FAO=∠BEO,∠AFO=∠EBO,又O为AE中点,根据AAS即可证明△AOF≌△EOB;
(2)根据平行四边形性质得出AD∥BC,根据平行线的性质及角平分线定义得出∠DAE=∠AEB=∠BAE,由等角对等边得到AB=BE,根据对角线互相平分的四边形是平行四边形得出四边形ABEF是平行四边形,根据菱形的判定推出即可;
(3)根据∠B=60°,AB=BE得出等边三角形ABE,推出AB=AE=CD,根据BC∥AD和CE≠AD得出梯形AECD,根据等腰梯形的判定推出即可.
(2)根据平行四边形性质得出AD∥BC,根据平行线的性质及角平分线定义得出∠DAE=∠AEB=∠BAE,由等角对等边得到AB=BE,根据对角线互相平分的四边形是平行四边形得出四边形ABEF是平行四边形,根据菱形的判定推出即可;
(3)根据∠B=60°,AB=BE得出等边三角形ABE,推出AB=AE=CD,根据BC∥AD和CE≠AD得出梯形AECD,根据等腰梯形的判定推出即可.
解答:(1)证明:∵?ABCD中,AD∥BC,
∴∠FAO=∠BEO,∠AFO=∠EBO.
在△AOF与△EOB中,
,
∴△AOF≌△EOB(AAS);
 (2)解:四边形ABEF是菱形,理由如下:
(2)解:四边形ABEF是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE.
由(1)知:△AOF≌△EOB,
∴OF=OB,
∵OA=OE,
∴四边形ABEF是平行四边形,
∵AB=BE,
∴平行四边形ABEF是菱形;
(3)解:当∠ABC为60度数时,四边形AECD是等腰梯形,理由如下:
∵AD∥BC,AD≠CE,
∴四边形AECD是梯形.
∵∠B=60°,由(2)知AB=BE,
∴△ABE是等边三角形,
∴AB=AE,
∵四边形ABCD是平行四边形,
∴AB=CD=AE,
∴梯形AECD是等腰梯形.
故答案为60°.
∴∠FAO=∠BEO,∠AFO=∠EBO.
在△AOF与△EOB中,
|
∴△AOF≌△EOB(AAS);
 (2)解:四边形ABEF是菱形,理由如下:
(2)解:四边形ABEF是菱形,理由如下:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE.
由(1)知:△AOF≌△EOB,
∴OF=OB,
∵OA=OE,
∴四边形ABEF是平行四边形,
∵AB=BE,
∴平行四边形ABEF是菱形;
(3)解:当∠ABC为60度数时,四边形AECD是等腰梯形,理由如下:
∵AD∥BC,AD≠CE,
∴四边形AECD是梯形.
∵∠B=60°,由(2)知AB=BE,
∴△ABE是等边三角形,
∴AB=AE,
∵四边形ABCD是平行四边形,
∴AB=CD=AE,
∴梯形AECD是等腰梯形.
故答案为60°.
点评:本题考查了平行四边形的性质,平行线的性质,全等三角形的判定与性质,角平分线定义,菱形的判定,等腰梯形的判定等知识点,主要考查学生的推理能力,题目综合性比较强,有一定的难度.

练习册系列答案
相关题目
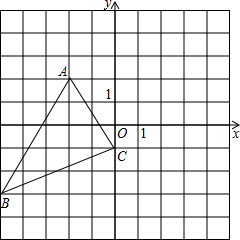 如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题: 如图,已知BC为⊙O的直径,A为⊙O上一点,连接AB、AC,BC=4,tanB=2,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于E点.
如图,已知BC为⊙O的直径,A为⊙O上一点,连接AB、AC,BC=4,tanB=2,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于E点.