题目内容
如果圆内接正方形的面积为36cm2,那么同圆外切正方形的面积等于 .
考点:正多边形和圆
专题:
分析:首先根据题意画出图形,由圆内接正方形的面积为36cm2,可求得其边长,继而求得此圆的半径,然后由等腰直角三角形的性质,求得同圆外切正方形的边长,继而求得答案.
解答: 解:如图,过点O作OB⊥CE,则OB⊥AF,连接OE,
解:如图,过点O作OB⊥CE,则OB⊥AF,连接OE,
∵圆内接正方形的面积为36cm2,
∴CE=6cm,∠COE=90°,
∴CD=
CE=3cm,∠COD=
∠COE=45°,
∴∠OCD=∠OAB=∠AOB=45°,
∴OD=CD=3cm,AB=OB,
∴OC=
=3
cm,
∴AB=OB=OC=3
cm,
∴AF=2AB=6
cm,
∴同圆外切正方形的面积等于:72cm2.
故答案为:72cm2.
 解:如图,过点O作OB⊥CE,则OB⊥AF,连接OE,
解:如图,过点O作OB⊥CE,则OB⊥AF,连接OE,∵圆内接正方形的面积为36cm2,
∴CE=6cm,∠COE=90°,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OCD=∠OAB=∠AOB=45°,
∴OD=CD=3cm,AB=OB,
∴OC=
| OD2+CD2 |
| 2 |
∴AB=OB=OC=3
| 2 |
∴AF=2AB=6
| 2 |
∴同圆外切正方形的面积等于:72cm2.
故答案为:72cm2.
点评:此题考查了正多边形与圆的知识.注意掌握等腰直角三角形的性质是关键,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
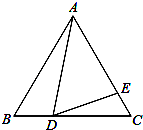 如图,在边长为9的等边△ABC中,BD=3,∠ADE=60°,求AE的长.
如图,在边长为9的等边△ABC中,BD=3,∠ADE=60°,求AE的长. 如图,已知AB=CD,AE=DF,CE=BF.
如图,已知AB=CD,AE=DF,CE=BF.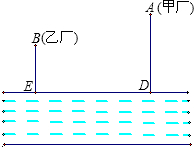 如图,大江的一侧有甲、乙两家工厂,它们都有垂直于江边的小路,长度分别为m千米和n千米,两条小路相距l千米.现在要在江边建一个抽水站,把水送到甲、乙两厂去.欲使供水管路最短,抽水站应建在哪里?
如图,大江的一侧有甲、乙两家工厂,它们都有垂直于江边的小路,长度分别为m千米和n千米,两条小路相距l千米.现在要在江边建一个抽水站,把水送到甲、乙两厂去.欲使供水管路最短,抽水站应建在哪里?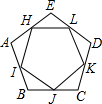 如图,H、I、J、K、L分别是正五边形ABCDE各边的中点,求证:五边形HIJKL是正五边形.
如图,H、I、J、K、L分别是正五边形ABCDE各边的中点,求证:五边形HIJKL是正五边形. 如图,点M把线段AB分成
如图,点M把线段AB分成