题目内容
抛物线y=
x2-kx+
与x轴的正方向相交于点A、B,顶点为C,若△ABC为等腰直角三角形,求k值及AB的长.
| 1 |
| 2 |
| 5 |
| 2 |
考点:抛物线与x轴的交点
专题:
分析:令y=0,得到关于x的一元二次方程,求出两根之和与两根之积表达式,然后求出AB的距离,求出函数的顶点坐标,利用等腰直角三角形的性质,令顶点纵坐标的绝对值等于AB的一半即可得到关于k的方程,通过解方程求得k的值.
解答:解:设A、B的坐标为(x1,0),(x2,0),
由
x2-kx+
=0,有x1+x2=2k,x1•x2=5,
∴|AB|=|x1-x2|=
=
=2
,
又∵-
=k,
=
,
∴顶点C的坐标为(k,
),
∵△ABC是等腰直角三角形,
∴|
|=
|AB|=
×2
,
∴k=±
.
则AB=2
,
综上所述,k值是±
,AB的长度是2
.
由
| 1 |
| 2 |
| 5 |
| 2 |
∴|AB|=|x1-x2|=
| (x1+x2)2-4x1•x2 |
| 4k2-20 |
| k2-5 |
又∵-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| 5-k2 |
| 2 |
∴顶点C的坐标为(k,
| 5-k2 |
| 2 |
∵△ABC是等腰直角三角形,
∴|
| 5-k2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k2-5 |
∴k=±
| 7 |
则AB=2
| 2 |
综上所述,k值是±
| 7 |
| 2 |
点评:本题考查了二次函数综合题,涉及函数与方程的关系、等腰直角三角形的性质、二次函数的最值等,要综合分析,认真解答.

练习册系列答案
相关题目
 如图,△ABC中,AB=AC,EF为过A的任一直线,CF⊥BC,BE⊥BC,求证:AE=AF.
如图,△ABC中,AB=AC,EF为过A的任一直线,CF⊥BC,BE⊥BC,求证:AE=AF. 在方框内填上正确的数.
在方框内填上正确的数.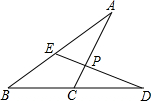 如图所示,已知∠A=20°,∠B=30°,AC⊥DE,求∠BED和∠D的度数.
如图所示,已知∠A=20°,∠B=30°,AC⊥DE,求∠BED和∠D的度数. 直线y=kx-4与x轴、y轴分别交于B、C两点,且
直线y=kx-4与x轴、y轴分别交于B、C两点,且