题目内容
4.(1)计算:$\sqrt{8}-4sin45°+{(3-π)^0}+|{\;-4\;}$|;(2)先化简,再求值:$(x+1-\frac{15}{x-1})÷\frac{x-4}{x-1}$,其中x=5$\sqrt{2}$-4.
分析 (1)原式第一项化为最简二次根式,第二项利用特殊角的三角函数值计算,第三项利用零指数幂法则计算,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:(1)原式=2$\sqrt{2}$-4×$\frac{\sqrt{2}}{2}$+1+4=5;
(2)原式=$\frac{(x+1)(x-1)-15}{x-1}$•$\frac{x-1}{x-4}$=$\frac{(x+4)(x-4)}{x-1}$•$\frac{x-1}{x-4}$=x+4,
当x=5$\sqrt{2}$-4时,原式=5$\sqrt{2}$-4+4=5$\sqrt{2}$.
点评 此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
3.化简$\sqrt{18}$的结果是( )
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{6}$ |
9. 如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
 如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
16.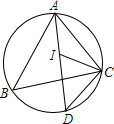 在△ABC中,∠ABC=60°,∠ACB=50°,如图所示,I是△ABC的内心,延长AI交△ABC的外接圆D,则∠ICD的度数是( )
在△ABC中,∠ABC=60°,∠ACB=50°,如图所示,I是△ABC的内心,延长AI交△ABC的外接圆D,则∠ICD的度数是( )
 在△ABC中,∠ABC=60°,∠ACB=50°,如图所示,I是△ABC的内心,延长AI交△ABC的外接圆D,则∠ICD的度数是( )
在△ABC中,∠ABC=60°,∠ACB=50°,如图所示,I是△ABC的内心,延长AI交△ABC的外接圆D,则∠ICD的度数是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
13.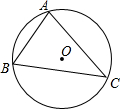 如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB=$\frac{3}{4}$,则⊙O的半径为( )
如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB=$\frac{3}{4}$,则⊙O的半径为( )
 如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB=$\frac{3}{4}$,则⊙O的半径为( )
如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB=$\frac{3}{4}$,则⊙O的半径为( )| A. | 4 | B. | 3 | C. | 2 | D. | $\sqrt{3}$ |
 如图,PA,PB是⊙O的两条切线,切点分别是A、B,PA=10,CD是⊙O的切线,交PA于点C,交PB于点D,则△PCD的周长是20.
如图,PA,PB是⊙O的两条切线,切点分别是A、B,PA=10,CD是⊙O的切线,交PA于点C,交PB于点D,则△PCD的周长是20.