题目内容
16.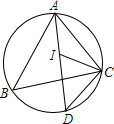 在△ABC中,∠ABC=60°,∠ACB=50°,如图所示,I是△ABC的内心,延长AI交△ABC的外接圆D,则∠ICD的度数是( )
在△ABC中,∠ABC=60°,∠ACB=50°,如图所示,I是△ABC的内心,延长AI交△ABC的外接圆D,则∠ICD的度数是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
分析 由三角形内角和定理求出∠BAC=70°,由I是△ABC的内心,得出∠BCD=∠BAD=$\frac{1}{2}$∠BAC=35°,∠BCI=$\frac{1}{2}$∠ACB=25°,求出∠BCD+∠BCI=60°即可.
解答 解:∵△ABC中,∠BAC=180°-∠ACB-∠ABC=180°-50°-60°=70°,
又∵I是△ABC的内心,
∴∠BCD=∠BAD=$\frac{1}{2}$∠BAC=35°,∠BCI=$\frac{1}{2}$∠ACB=25°,
∴∠BCD+∠BCI=35°+25°=60°,
即∠ICD=60°,
故选:C
点评 本题考查了三角形的内心的性质、三角形内角和定理、圆周角定理;熟练掌握三角形内心的性质和圆周角定理是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图所示的几何体,其主视图是( )
如图所示的几何体,其主视图是( )
 如图所示的几何体,其主视图是( )
如图所示的几何体,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
8. 为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:
为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:
学业考试体育成绩(分数段)统计表
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为60,b的值为0.15,并将统计图补充完整;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数.”请问:甲同学的体育成绩应在什么分数段内?C(填相应分数段的字母).
(3)如果把成绩在45分以上(含45分)定为优秀,那么该县2015年4020名九年级学生中体育成绩为优秀的学生人数约有多少名?
 为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:
为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:学业考试体育成绩(分数段)统计表
| 分数段 | 人数(人) | 频率 |
| A | 12 | 0.05 |
| B | 36 | b |
| C | 84 | 0.35 |
| D | a | 0.25 |
| E | 48 | 0.2 |
(1)在统计表中,a的值为60,b的值为0.15,并将统计图补充完整;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数.”请问:甲同学的体育成绩应在什么分数段内?C(填相应分数段的字母).
(3)如果把成绩在45分以上(含45分)定为优秀,那么该县2015年4020名九年级学生中体育成绩为优秀的学生人数约有多少名?
6.如果分式$\frac{|x|-1}{2x+2}$的值为0,则x的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | ±1 |
 小明家住房的结构如图所示(图形均为长方形,单位:米),小明爸爸打算把卧室以外的部分都铺上地板砖,请问
小明家住房的结构如图所示(图形均为长方形,单位:米),小明爸爸打算把卧室以外的部分都铺上地板砖,请问 如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于D,连接AD、OD(AC≠AB),则能够判断图中∠B的余角(不再添加任何辅助线)的有( )
如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于D,连接AD、OD(AC≠AB),则能够判断图中∠B的余角(不再添加任何辅助线)的有( ) 如图,直线PA经过点A(-1,0)、点P(1,2),直线PB是一次函数y=-x+3的图象.
如图,直线PA经过点A(-1,0)、点P(1,2),直线PB是一次函数y=-x+3的图象.