题目内容
13．
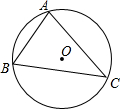如图，⊙O是△ABC的外接圆，弦AC的长为3，sinB=$\frac{3}{4}$，则⊙O的半径为（ ）| A． | 4 | B． | 3 | C． | 2 | D． | $\sqrt{3}$ |
分析 作直径AD，连接CD，根据正弦的概念求出∠D的正弦，根据圆周角定理得到∠B=∠D，得到答案．
解答 解：
作直径AD，连接CD，
∴∠D=∠B，
∴sinD=sinB=$\frac{3}{4}$，
在直角△ADC中，AC=3，
∴AD=$\frac{AC}{sinD}$=4，
∴⊙O的半径为2．
故选C．
点评 本题考查的是圆周角定理和解直角三角形的知识，正确作出辅助线、构造直角三角形是解题的关键，注意锐角三角函数的概念的运用．
练习册系列答案
相关题目
11．若2x=3y，则$\frac{2x+y}{x-3y}$的值是（ ）
| A． | -1 | B． | $-\frac{8}{3}$ | C． | 1 | D． | $\frac{8}{3}$ |
1．
如图所示的几何体，其主视图是（ ）
如图所示的几何体，其主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
8．
为了解我省2015届九年级学生学业水平考试体育成绩，现从中随机抽取部分学生的体育成绩进行分段（A：0-29分；B：30-39分；C：40-44分；D：45-49分；E：50分）统计如下：
学业考试体育成绩（分数段）统计表
根据上面提供的信息，回答下列问题：
（1）在统计表中，a的值为60，b的值为0.15，并将统计图补充完整；
（2）甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数．”请问：甲同学的体育成绩应在什么分数段内？C（填相应分数段的字母）．
（3）如果把成绩在45分以上（含45分）定为优秀，那么该县2015年4020名九年级学生中体育成绩为优秀的学生人数约有多少名？
为了解我省2015届九年级学生学业水平考试体育成绩，现从中随机抽取部分学生的体育成绩进行分段（A：0-29分；B：30-39分；C：40-44分；D：45-49分；E：50分）统计如下：学业考试体育成绩（分数段）统计表
| 分数段 | 人数（人） | 频率 |
| A | 12 | 0.05 |
| B | 36 | b |
| C | 84 | 0.35 |
| D | a | 0.25 |
| E | 48 | 0.2 |
（1）在统计表中，a的值为60，b的值为0.15，并将统计图补充完整；
（2）甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数．”请问：甲同学的体育成绩应在什么分数段内？C（填相应分数段的字母）．
（3）如果把成绩在45分以上（含45分）定为优秀，那么该县2015年4020名九年级学生中体育成绩为优秀的学生人数约有多少名？
18．
将三角形纸片（△ABC）按如图所示的方式折叠，使点C落在AB边上的点D，折痕为EF．已知AB=AC=3，BC=4，若以点B、D、F为顶点的三角形与△ABC相似，那么CF的长度是（ ）
将三角形纸片（△ABC）按如图所示的方式折叠，使点C落在AB边上的点D，折痕为EF．已知AB=AC=3，BC=4，若以点B、D、F为顶点的三角形与△ABC相似，那么CF的长度是（ ）| A． | 2 | B． | $\frac{12}{7}$或2 | C． | $\frac{12}{7}$ | D． | $\frac{12}{5}$或2 |
如图，直线PA经过点A（-1，0）、点P（1，2），直线PB是一次函数y=-x+3的图象．