题目内容
13.在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同.小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下的三个小球中随机取出一个小球,记下数字为y.(1)画树状图或列表,写出Q点所有坐标.
(2)计算由x、y确定的点Q(x,y)在函数y=-x+5图象上的概率;
(3)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜.
这个游戏公平吗?说明理由;若不公平,怎么修改规则才对双方公平?
分析 (1)先画树状图可展示所有12种等可能的结果数;
(2)根据一次函数图象上点的坐标特征,从12种情况中找出在函数y=-x+5图象上的点的个数,然后根据概率公式求解;
(3)先分别计算出小明胜和小红胜的概率,再根据概率的大小关系可判断这种游戏方案设计对双方不公平,然后修改规则,使小明获胜的概率等于小红获胜的概率即可.
解答 解:(1)画树状图为:
共有12种等可能的结果数,它们是:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)
(2)点(1,4),(2,3),(3,2),(4,1)在函数y=-x+5图象上,
所以点Q(x,y)在函数y=-x+5图象上的概率=$\frac{4}{12}$=$\frac{1}{3}$;
(3)这个游戏不公平.理由如下:
P(小明胜)=$\frac{4}{12}$=$\frac{1}{3}$,P(小红胜)=$\frac{6}{12}$=,
∵P(小明胜)<P(小红胜).
∴这种游戏方案设计对双方不公平.
这个游戏规则可改为:若x、y满足xy≥6,则小明胜;若x、y满足xy<6,则小红胜.
点评 本题考查了游戏的公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.也考查了列表法与树状图法.

练习册系列答案
相关题目
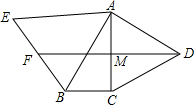 如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,F是BE的中点,DF交AC于M,试说明线段AM与MC相等的理由.
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,F是BE的中点,DF交AC于M,试说明线段AM与MC相等的理由.