题目内容
2．
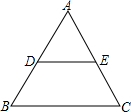如图，等边△ABC中，点D、E分别为边AB、AC的中点，则∠DEC的度数为120°．
分析 根据等边三角形的性质，可得∠C的度数，根据三角形中位线的性质，可得DE与BC的关系，根据平行线的性质，可得答案．
解答 解：∵△ABC是等边三角形，
∴∠C=60°，
∵点D、E分别为边AB、AC的中点，
∴DE∥BC，
∴∠DEC=180°-∠C=180°-60°=120°，
故答案为：120°．
点评 本题考查了三角形中位线定理以及等边三角形的性质，解题的关键是掌握三角形的中位线平行于第三边且等于第三边的一半．
练习册系列答案
相关题目
12．
如图所示的立体图形的主视图是（ ）
如图所示的立体图形的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
13．某工厂对一个小组生产的零件进行调查．在10天中，这个小组出次品的情况如表所示：
那么在这10天中这个小组每天所出次品数的标准差是$\sqrt{2}$．
| 每天出次品的个数 | 0 | 2 | 3 | 4 |
| 天数 | 3 | 2 | 4 | 1 |
如图，在△ABC中，点E、F分别在边AC、BC上，EF∥AB，CE=$\frac{1}{2}$AE，若$\overrightarrow{AC}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，则$\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$．
如图，△ABC中，AB=AC，点D，E在BC边上，当BD=CE时，△ABD≌△ACE．（添加一个适当的条件即可）
7．
如图，已知直线a，b被直线c所截，那么∠1的同位角是（ ）
如图，已知直线a，b被直线c所截，那么∠1的同位角是（ ）| A． | ∠5 | B． | ∠4 | C． | ∠3 | D． | ∠2 |
如果按图中虚线对折可以做成一个上底面为无盖的盒子，那么该盒子的下底面的字母是B．
12．若$\sqrt{2}$的整数部分为a，小数部分为b，则a-b的值为（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | 2-$\sqrt{2}$ | D． | 2+$\sqrt{2}$ |