题目内容
7.若关于x的方程x2+2mx+m2+3m-2=0有两个实数根x1、x2,则x1(x2+x1)+x22的最小值为( )| A. | 1 | B. | 2 | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
分析 根据判别式的意义得到m≤$\frac{2}{3}$,再利用根与系数的关系得到x1+x2=-2m,x1x2=m2+3m-2,所以x1(x2+x1)+x${\;}_{2}^{2}$=(x2+x1)2-x1x2=3m2-3m+2,利用配方法得到原式=3(m-$\frac{1}{2}$)2+$\frac{5}{4}$,然后利用非负数的性质可判断x1(x2+x1)+x${\;}_{2}^{2}$的最小值为$\frac{5}{4}$.
解答 解:根据题意得△=4m2-4(m2+3m-2)≥0,解得m≤$\frac{2}{3}$
x1+x2=-2m,x1x2=m2+3m-2,
x1(x2+x1)+x${\;}_{2}^{2}$=(x2+x1)2-x1x2
=4m2-(m2+3m-2)
=3m2-3m+2
=3(m-$\frac{1}{2}$)2+$\frac{5}{4}$,
所以m=$\frac{1}{2}$时,x1(x2+x1)+x${\;}_{2}^{2}$有最小值,最小值为$\frac{5}{4}$.
故选D.
点评 本题考查了根与系数的关系:若x1,x2是方程ax2+bx+c=0的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也可考查了非负数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
 某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )| A. | 从图中可以直接看出喜欢各种球类的具体人数 | |
| B. | 从图中可以直接看出全班的总人数 | |
| C. | 从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况 | |
| D. | 从图中可以直接看出全班同学现在喜欢各种球类人数的大小关系 |
12.若$\sqrt{2}$的整数部分为a,小数部分为b,则a-b的值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2-$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |
19.若甲数为x,乙数为y,则“甲数的3倍比乙数的一半少2”,列成方程是( )
| A. | 3x$+\frac{1}{2}$y=2 | B. | $\frac{1}{2}y-3x$=2 | C. | 3x$-\frac{1}{2}y$=2 | D. | $\frac{1}{2}y$+2=3x |
 如图,△ABC中,AB=AC,点D,E在BC边上,当BD=CE时,△ABD≌△ACE.(添加一个适当的条件即可)
如图,△ABC中,AB=AC,点D,E在BC边上,当BD=CE时,△ABD≌△ACE.(添加一个适当的条件即可)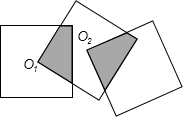 如图,三个边长均为4的正方形重叠在一起,O1,O2是其中两个正方形的对角线交点,则阴影部分面积是8.
如图,三个边长均为4的正方形重叠在一起,O1,O2是其中两个正方形的对角线交点,则阴影部分面积是8.