题目内容
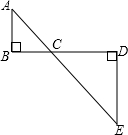 如图,C为线段BD上的一个动点,分别过点B,D在BD两侧作AB⊥BD,ED⊥BD,连结AC,EC.已知AB=5,DE=9,BD=8,设CD=x.
如图,C为线段BD上的一个动点,分别过点B,D在BD两侧作AB⊥BD,ED⊥BD,连结AC,EC.已知AB=5,DE=9,BD=8,设CD=x.(1)用含x的代数式表示AC+CE的长;
(2)请问:点C满足什么条件时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式
| x2+4 |
| (12-x)2+9 |
考点:轴对称-最短路线问题,二次根式的应用
专题:
分析:(1)由于△ABC和△CDE都是直角三角形,故AC,CE可由勾股定理求得;
(2)若点C不在AE的连线上,根据三角形中任意两边之和>第三边知,AC+CE>AE,故当A、C、E三点共线时,AC+CE的值最小;
(3)由(1)(2)的结果可作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连接AE交BD于点C,则AE的长即为代数式
+
的最小值,然后构造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性质可求得AE的值.
(2)若点C不在AE的连线上,根据三角形中任意两边之和>第三边知,AC+CE>AE,故当A、C、E三点共线时,AC+CE的值最小;
(3)由(1)(2)的结果可作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连接AE交BD于点C,则AE的长即为代数式
| x2+4 |
| (12-x)2+9 |
解答:解:(1)∵AC=
=
,
CE=
=
,
∴AC+CE=
+
;
(2)当A、C、E三点共线时,AC+CE的值最小;
(3)如右图所示,作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连接AE交BD于点C,
设BC=x,则AE的长即为代数的
+
的最小值.
过点A作AF∥BD交ED的延长线于点F,得矩形ABDF,
则AB=DF=2,AF=BD=12,EF=ED+DF=3+2=5,
所以AE=
=
=13,
即
+
的最小值为13.
| AB2+BC2 |
| 25+(8-x)2 |
CE=
| CD2+DE2 |
| x2+81 |
∴AC+CE=
| x2+81 |
| 25+(8-x)2 |
(2)当A、C、E三点共线时,AC+CE的值最小;
(3)如右图所示,作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连接AE交BD于点C,

设BC=x,则AE的长即为代数的
| x2+4 |
| (12-x)2+9 |
过点A作AF∥BD交ED的延长线于点F,得矩形ABDF,
则AB=DF=2,AF=BD=12,EF=ED+DF=3+2=5,
所以AE=
| AF2+EF2 |
| 122+52 |
即
| x2+4 |
| (12-x)2+9 |
点评:此题主要考查了轴对称求最短路径,本题利用了数形结合的思想,求形如
+
的式子的最小值,可通过构造直角三角形,利用勾股定理求解.
| x2+4 |
| (12-x)2+9 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某商店举办有奖销售活动,活动规则如下:凡购满100元者得奖券一张,每1000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个.那么,买100元商品的中奖概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 在图中,将大写字母“N”绕它右下侧的顶点按顺时针方向旋转90°,作出旋转后的图案.
在图中,将大写字母“N”绕它右下侧的顶点按顺时针方向旋转90°,作出旋转后的图案. 如图,AB是半圆O的直径,AE为弦,C为
如图,AB是半圆O的直径,AE为弦,C为
 如图,一根5m长的绳子,一端拴在柱子上,另一端栓着一只羊,请画出羊的活动区域.
如图,一根5m长的绳子,一端拴在柱子上,另一端栓着一只羊,请画出羊的活动区域.