题目内容
把下列各式因式分解:
(1)8y4-2y2;
(2)4(2p+3q)2-(3p-q)2;
(3)-(m-n)2+1;
(4)36m2(a+b)2-25m2(a-b)2.
(1)8y4-2y2;
(2)4(2p+3q)2-(3p-q)2;
(3)-(m-n)2+1;
(4)36m2(a+b)2-25m2(a-b)2.
考点:提公因式法与公式法的综合运用
专题:
分析:(1)首先提取公因式进而利用平方差公式分解因式即可;
(2)直接利用平方差公式分解因式即可;
(3)直接利用平方差公式分解因式即可;
(4)首先提取公因式进而利用平方差公式分解因式即可.
(2)直接利用平方差公式分解因式即可;
(3)直接利用平方差公式分解因式即可;
(4)首先提取公因式进而利用平方差公式分解因式即可.
解答:解:(1)8y4-2y2
=2y2(4y2-1)
=2y2(2y-1)(2y+1);
(2)4(2p+3q)2-(3p-q)2,
=[2(2p+3q)+3p-q][2(2p+3q)-(3p-q)]
=(7p+5q)(p+7q);
(3)-(m-n)2+1=(1+m-n)(1-m+n);
(4)36m2(a+b)2-25m2(a-b)2
=m2[6(a+b)+5(a-b)][6(a+b)-5(a-b)]
=m2(11a+b)(a+11b).
=2y2(4y2-1)
=2y2(2y-1)(2y+1);
(2)4(2p+3q)2-(3p-q)2,
=[2(2p+3q)+3p-q][2(2p+3q)-(3p-q)]
=(7p+5q)(p+7q);
(3)-(m-n)2+1=(1+m-n)(1-m+n);
(4)36m2(a+b)2-25m2(a-b)2
=m2[6(a+b)+5(a-b)][6(a+b)-5(a-b)]
=m2(11a+b)(a+11b).
点评:此题主要考查了利用提取公因式法以及公式法分解因式,正确记忆平方差公式是解题关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
若b是a和c的比例中项,则关于x的一元二次方程ax2+2bx+c=0的根的情况是( )
| A、有两个相等的实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、无法判断 |

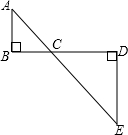 如图,C为线段BD上的一个动点,分别过点B,D在BD两侧作AB⊥BD,ED⊥BD,连结AC,EC.已知AB=5,DE=9,BD=8,设CD=x.
如图,C为线段BD上的一个动点,分别过点B,D在BD两侧作AB⊥BD,ED⊥BD,连结AC,EC.已知AB=5,DE=9,BD=8,设CD=x. 如图,两幢建筑物的水平距离为32.6m,从点A测得点D的俯角α=35°12′,测得点C的俯角β为43°24′,求这两幢建筑物的高(结果精确到0.1m).
如图,两幢建筑物的水平距离为32.6m,从点A测得点D的俯角α=35°12′,测得点C的俯角β为43°24′,求这两幢建筑物的高(结果精确到0.1m).