题目内容
16.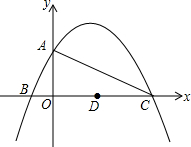 如图,已知二次函数y=-$\frac{1}{4}$x2+$\frac{3}{2}x$+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
如图,已知二次函数y=-$\frac{1}{4}$x2+$\frac{3}{2}x$+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.(1)点A的坐标为(0,4),点C的坐标为(8,0);
(2)将△AOC绕点D顺时针旋转90°得△PMN,A点对应的点为P点,判断点P是否在该抛物线上;
(3)在抛物线上是否存在点E,使得△EDC的面积为△OAC面积的$\frac{5}{8}$?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由.
分析 (1)根据自变量与函数值的对应关系,可得A、C点坐标;
(2)根据旋转的性质,可得M点、P点坐标,根据代入法将P点坐标代入,可得答案;
(3)根据三角形的面积,可得E点的纵坐标,根据自变量与函数值的对应关系,可得关于x的方程,根据解方程,可得答案.
解答 解:(1)当y=0时,-$\frac{1}{4}$x2+$\frac{3}{2}x$+4=0,
解得x1=8,x2=-2(不符合题意的解要舍去),即C(8,0),
当x=0时,y=4,即A(0,4),
故答案为:(0,4),(8,0);
(2)如图 ,由旋转的性质,得
,由旋转的性质,得
DM=OD=3,DM⊥x轴,即M(3,3),
MP=OA=4,4+3=7,即P(7,3),
当x=7时,y=-$\frac{1}{4}$×72+$\frac{3}{2}$×7+4=2≠3,
P点不在抛物线的图象上;
(3)OA=4,OC=8,DC=8-4=4,
S△AOC=$\frac{1}{2}$OA•OC=$\frac{1}{2}$×8×4=16,
S△EDC=$\frac{1}{2}$DC•|yE|=$\frac{5}{8}$×S△AOC=10,
|yE|=4,
解得y=4或y=-4,
当y=4时,-$\frac{1}{4}$x2+$\frac{3}{2}x$+4=4,化简得x2-6x=0,解得x1=6,x2=0,即E1(6,4),E2(0,4);
当y=-4时,-$\frac{1}{4}$x2+$\frac{3}{2}x$+4=-4,化简,得x2-6x-32=0,解得x1=3+$\sqrt{41}$,x2=3-$\sqrt{41}$,即E3(3+$\sqrt{41}$,-4),E4(3-$\sqrt{41}$,-4),
综上所述:E1(6,4),E2(0,4);E3(3+$\sqrt{41}$,-4),E4(3-$\sqrt{41}$,-4).
点评 本题考查了二次函数综合题,(1)利用自变量与函数值的对应关系得出点的坐标;(2)利用旋转的性质得出P点坐标是解题关键,又利用了点的坐标满足函数解析式点在函数图象上;(3)利用三角形的面积的出关x的方程是解题关键.

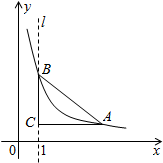 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=2.将BC边在直线l上滑动,使A、B在函数$y=\frac{k}{x}$的图象上.那么k的值是( )
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=2.将BC边在直线l上滑动,使A、B在函数$y=\frac{k}{x}$的图象上.那么k的值是( )| A. | $\frac{15}{4}$ | B. | 6 | C. | $\frac{5}{2}$ | D. | 3 |
| A. |  | B. |  | C. |  | D. |  |
| A. | a=-3,b=1 | B. | a=3,b=1 | C. | a=$\frac{3}{2}$,b=-1 | D. | a=-$\frac{3}{2}$,b=1 |
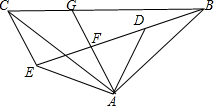 如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,下面结论正确的是①③④(填序号).
如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,下面结论正确的是①③④(填序号).