题目内容
14.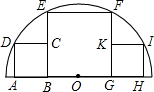 如图,三个相邻的正方形内接于半圆,若小正方形的面积为16cm2,则正方形BEFG的边长为( )
如图,三个相邻的正方形内接于半圆,若小正方形的面积为16cm2,则正方形BEFG的边长为( )| A. | 4cm | B. | 8cm | C. | 4$\sqrt{5}$cm | D. | 6$\sqrt{2}$cm |
分析 已知小正方形的面积即可求得边长,在RT△AOD和RT△BOE中,利用勾股定理即可求解.
解答  解:如图,连接OD、OE,
解:如图,连接OD、OE,
设大正方形的边长为2x,圆的半径为R,
∵大正方形有两个顶点在半圆上,另外两个顶点在圆心两侧,
∴BO=GO=x,BE=2x;
∵小正方形的面积为16cm2,
∴小正方形的边长AB=AD=4,
由勾股定理得,R2=OB2+BE2=OA2+AD2,
即x2+4x2=(x+4)2+42,
解得,x=4,则边长BG=2x=8.
故选B.
点评 本题考查了勾股定理的运用和正方形的性质,解题的关键是正确的做出辅助线构造直角三角形.

练习册系列答案
相关题目
2.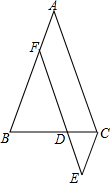 如图,在△ABC中,AB=AC,点D在边BC上,过点D作DF∥AC交AB于点F,过点C作CE∥AB交FD的延长线于点E.则下列结论正确的是( )
如图,在△ABC中,AB=AC,点D在边BC上,过点D作DF∥AC交AB于点F,过点C作CE∥AB交FD的延长线于点E.则下列结论正确的是( )
 如图,在△ABC中,AB=AC,点D在边BC上,过点D作DF∥AC交AB于点F,过点C作CE∥AB交FD的延长线于点E.则下列结论正确的是( )
如图,在△ABC中,AB=AC,点D在边BC上,过点D作DF∥AC交AB于点F,过点C作CE∥AB交FD的延长线于点E.则下列结论正确的是( )| A. | DC+DF=AB | B. | BD+DC=DF | C. | CE+DF=AB | D. | CE+DC=BD |
3.若-x2yn与3yx2是同类项,则n的值是( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
4.下列运算正确的是( )
| A. | (π-3.14)0=0 | B. | (π-3.14)0=1 | C. | ($\frac{1}{2}$)-1=-2 | D. | ($\frac{1}{2}$)-1=-$\frac{1}{2}$ |
 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2-4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0;其中正确的个数有2个.
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2-4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0;其中正确的个数有2个. 如图,已知AD∥BE,∠1=∠2,请判断∠A与∠E是否相等?并说明理由.
如图,已知AD∥BE,∠1=∠2,请判断∠A与∠E是否相等?并说明理由.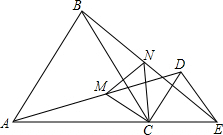 如图,△ABC、△DEC均为等边三角形,点M为线段AD的中点,点N为线段BE的中点,求证:△CNM为等边三角形.
如图,△ABC、△DEC均为等边三角形,点M为线段AD的中点,点N为线段BE的中点,求证:△CNM为等边三角形.